Chapter 2 Statistical Learning

2.1 2.1 What Is Statistical Learning?

Motivating example:

Suppose that we are statistical consultants hired by a client to provide advice on how to improve sales of a particular product. … our goal is to develop an accurate model that can be used to predict sales on the basis of the three media budgets.

glimpse(Advertising)

## Rows: 200
## Columns: 4
## $ TV        <dbl> 230.1, 44.5, 17.2, 151.5, 180.8, 8.7, 57.5, 120.2, 8.6, 199.…
## $ radio     <dbl> 37.8, 39.3, 45.9, 41.3, 10.8, 48.9, 32.8, 19.6, 2.1, 2.6, 5.…
## $ newspaper <dbl> 69.2, 45.1, 69.3, 58.5, 58.4, 75.0, 23.5, 11.6, 1.0, 21.2, 2…
## $ sales     <dbl> 22.1, 10.4, 9.3, 18.5, 12.9, 7.2, 11.8, 13.2, 4.8, 10.6, 8.6…

Advertising %>%
    ggplot(mapping = aes(x = TV, y = sales)) +
    geom_point(alpha = 0.25, shape = 1) + 
    theme_bw() +
    geom_smooth(formula = y~x, method = "lm", se = FALSE)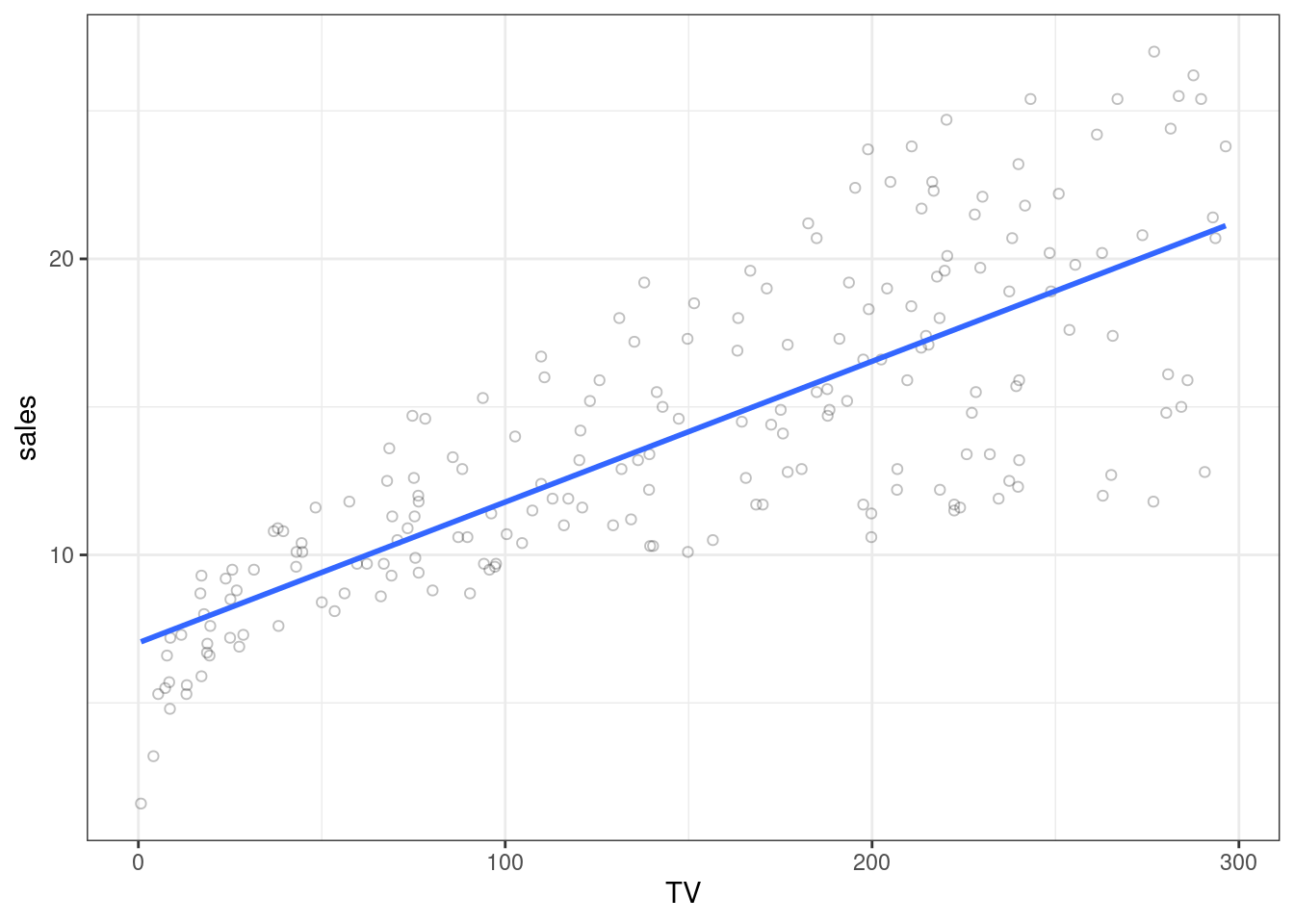

Advertising %>%
    ggplot(mapping = aes(x = radio, y = sales)) +
    geom_point(alpha = 0.25, shape = 1) + 
    theme_bw() +
    geom_smooth(formula = y~x, method = "lm", se = FALSE)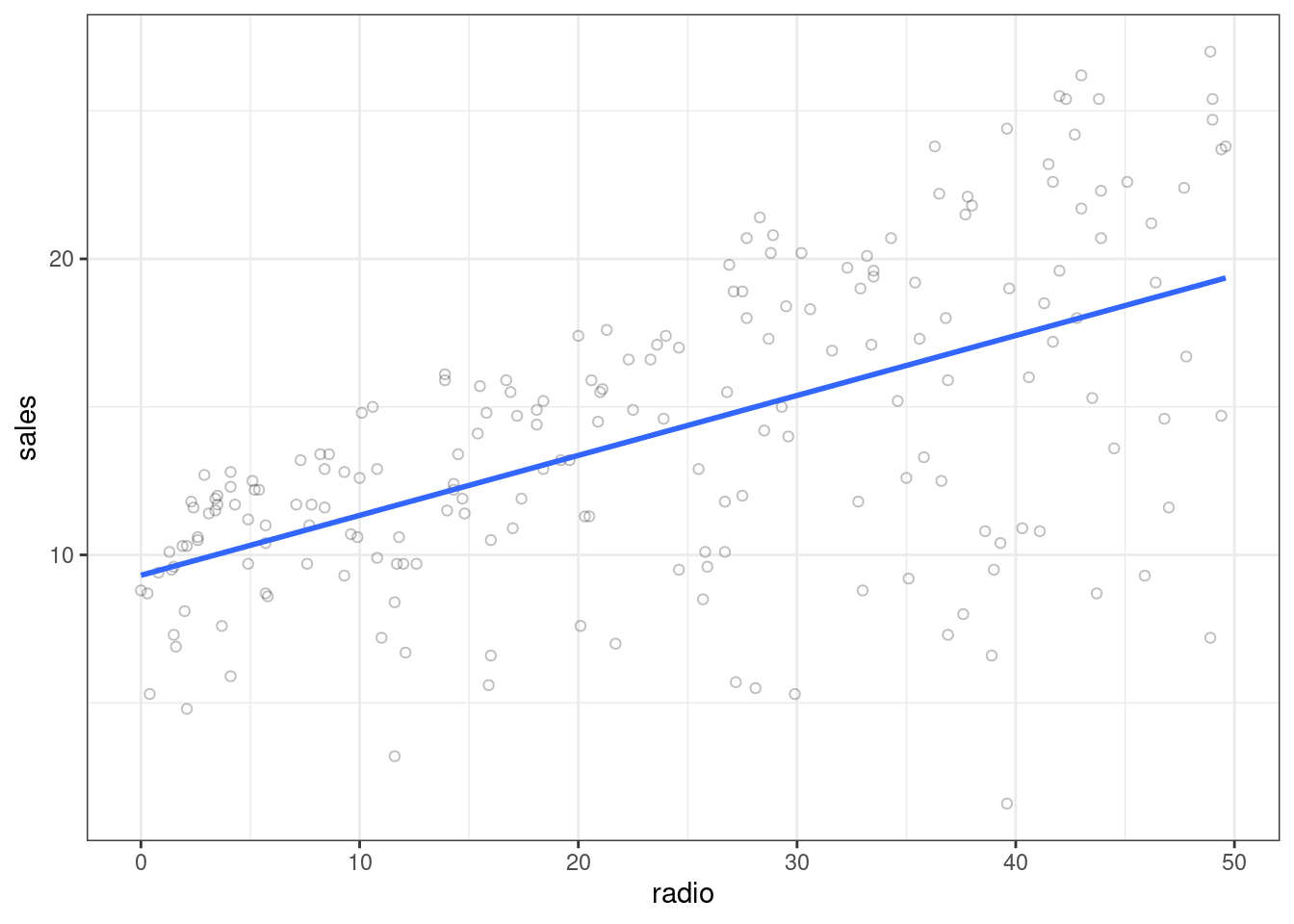

Advertising %>%
    ggplot(mapping = aes(x = newspaper, y = sales)) +
    geom_point(alpha = 0.25, shape = 1) + 
    theme_bw() +
    geom_smooth(formula = y~x, method = "lm", se = FALSE)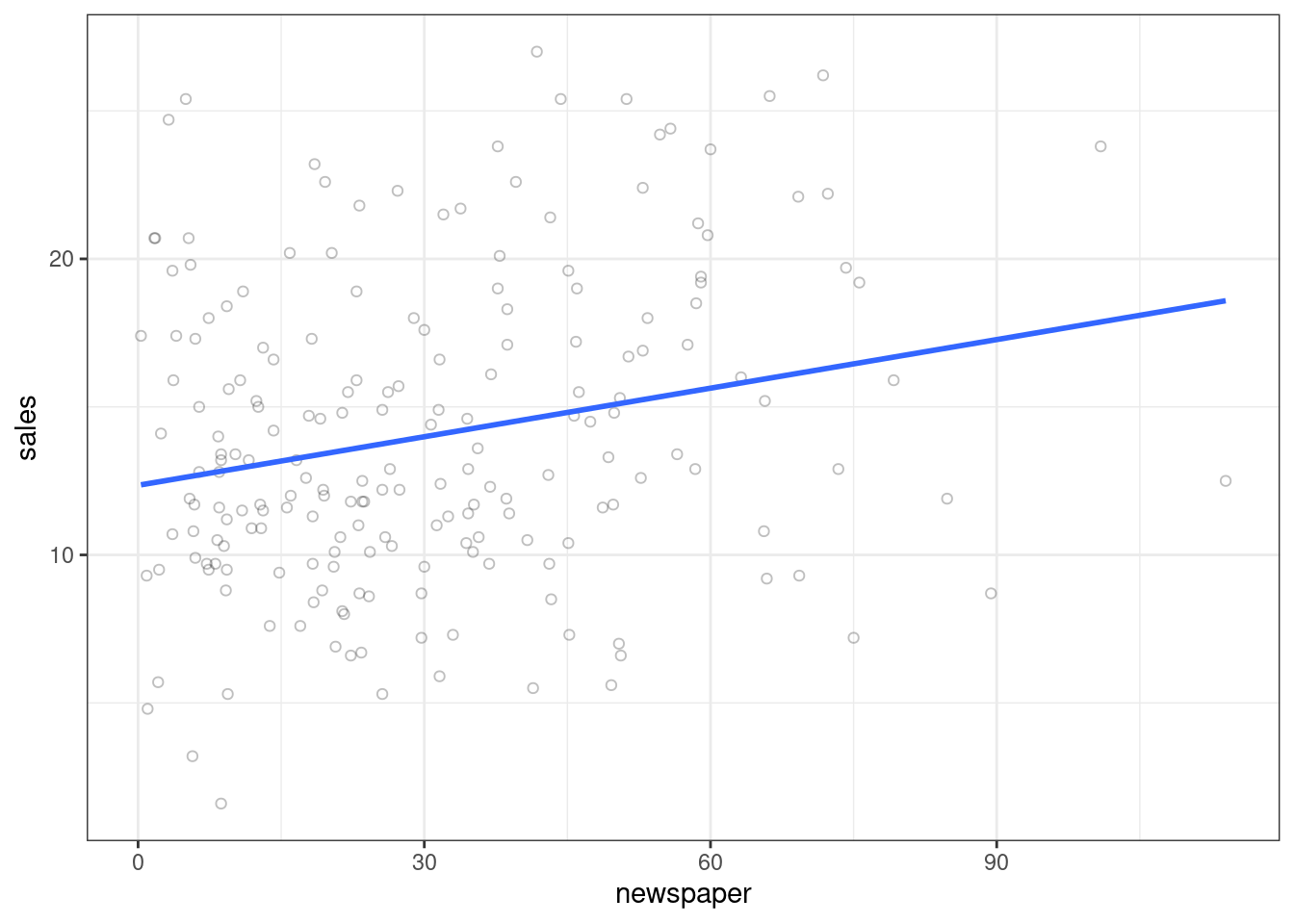

Input Variables: These are the variables we know and can use to build our model. Also known as predictors, independent variables, or features. Denoted using the symbol \(X_n\).

Output Variable: This is the variable we are trying to predict with the model. Also known as a response, or dependent variable. Typically denoted as \(Y\).

More generally: \(Y = f(X) + \epsilon\)

Where \(Y\) is the quantitative response and \(f\) is a function of \(X_1, ..., X_p\) (of \(p\) different predictors) and \(\epsilon\) is some random error term.

Assumptions:

\(f\) is systematic in its relationship to \(Y\)
\(\epsilon\) is independent of \(X\)
\(\epsilon\) has mean zero

Another example: Income and education may appear related, but the exact relationship is unknown. Note that some of the observations are above the linear interpolated line, while some are below it. The difference is \(\epsilon\)

Income1 %>%
    ggplot(mapping = aes(x = Education, y = Income)) +
    geom_point(color = "red") + 
        geom_smooth(formula = y~x, method = "lm", se = FALSE) +
    theme_bw()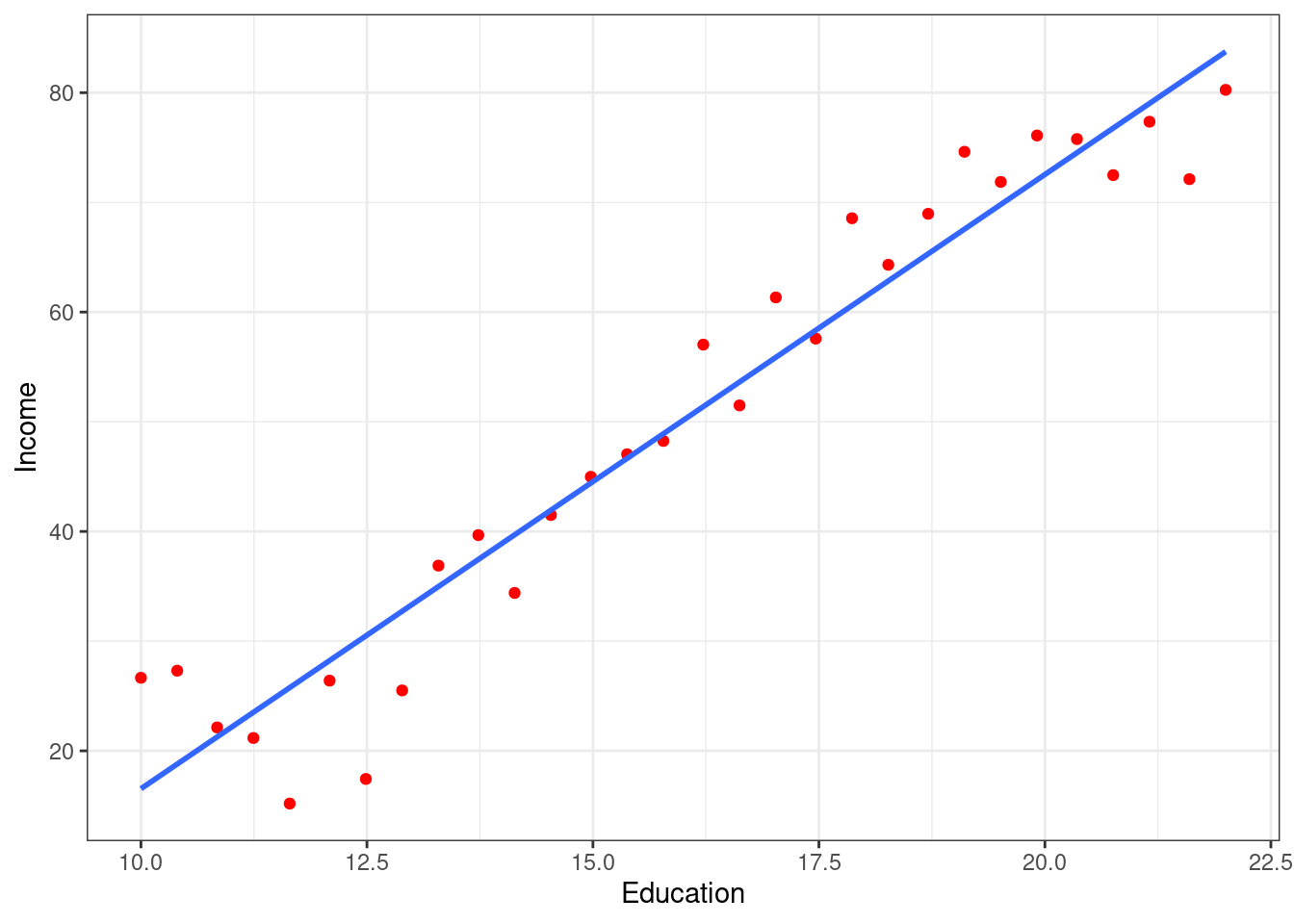

2.1.1 2.1.1 Why Estimate f?

There are two main reasons to estimate \(f\):

Prediction
Inference

2.1.1.1 Prediction

Consider: \(\hat{Y} = \hat{f}(X)\)

If \(X\) is known, we can predict \(\hat{Y}\) by this equation. Don’t be too concerned with the exact functional form of \(\hat{f}\), as long as it yields accurate predictions of \(Y\).

The accuracy of \(\hat{Y}\) depends on two quantities:

Reducible error: This is error that comes with the model. We can potentially address this error by improving the accuracy of the model.
Irreducible error: This is error introduced to the model, because \(\epsilon\), by definition, cannot be explained by \(X\)

Why is irreducible error larger than zero? Consider the estimate \(\hat{f}\) and a prediction \(\hat{Y} = \hat{f}(X)\). Let \(\hat{f}\) and \(X\) be fixed. Then:

\[ E(Y - Y^2) = E[f(X) + \epsilon - \hat{f}(X)]^2 \] \[ = [f(X) - \hat{f}(X)]^2 + Var(\epsilon) \]

Where \(E(Y - Y^2)\) is the expected value of the squared difference between the predicted and actual value of \(Y\), and \(Var(X)\) is the variance associated with the error term \(\epsilon\).

2.1.1.2 Inference:

When used for inference, the aim is not to use estimate \(f\) for predictions, but rather to understand how some response \(Y\) is affected by the changes in \(X_1, ..., X_p\).

Which predictors are associated with the response?: Identifying the important predictors is the aim here.
What is the relationship between the response and each predictor?: This can be positive, negative, or depend on the values of other predictors, depending on how complicated the model is.
Can the relationship between \(Y\) and each predictor be summarized using a linear equation?

Examples:

Prediction: A Company using a model to identify target customers for a direct-marketing campaign. The company is not interested in the model, they just want a function form that will help them.

Inference: Modeling customer purchases of specific brands of products. The model is aimed toward explaining which components of the model affect probability of a purchase.

Functional form: In many cases, a linear model allows for a relatively interpretable form, but may not be as flexible or accurate as other models.

2.1.2 2.1.2 How Do We Estimate \(f\)?

There are many different approaches to estimating \(f\), which all share certain characteristics and terms.

Training Data: This is the data used to train or teach our model how to estimate \(\hat{f}\). In general, most estimation methods can be characterized as either parametric or non-parametric.

2.1.2.1 Parametric Methods:

Involves a two-step model-base approach:

Assume functional form.

Example: \(f(X) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... + \beta_p X_p\) (This is a linear model)

After model selection, identify the procedure to estimate the parameters of the model. For linear models, this would be the method of estimating \(\beta_0\), \(\beta_1\), … etc such that:

\[ Y \approx \beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... + \beta_p X_p \]

The most common approach with linear models is the (Ordinary) least squares method. The parametric method reduces estimation to determining a set of parameters that create the best fit for an assumed functional form.

Pros:

Assuming the form makes estimation simpler!

Potential Cons:

We don’t know the true \(f\), and we could be way off!
We can choose more flexible models to address this, but…
More flexible models lead to more parameters to estimate, and potentially overfitting.

2.1.2.2 Non-parametric Methods

Pro: Do not make assumptions about functional form.

Con: Require a large number of observations to obtain an estimate of \(f\)

2.1.3 2.1.3 The Trade-Off Between Prediction Accuracy and Model Interpretability

plot(0:10,
     type = 'n',
    xlim = c(0, 10),
    xaxt = 'none',
    ylim = c(0, 10),
    yaxt = 'none',
    xlab = "Flexibility", 
    ylab = "Interpretability")
axis(1, at = c(1, 8.75), labels = c("Low", "High"))
axis(2, at = c(1, 8.75), labels = c("Low", "High"))
text(x=1, y=9.5, "Subset Selection", font=1)
text(x=1, y=8.5, "Lasso", font=1)
text(x=3.25, y=6.75, "Least Squares", font=1)
text(x=4.75, y=5, "Generalized Additive Models", font=1)
text(x=4.75, y=4.5, "Trees", font=1)
text(x=8.75, y=3, "Bagging, Boosting", font=1)
text(x=7.5, y=1.25, "Support Vector Machines", font=1)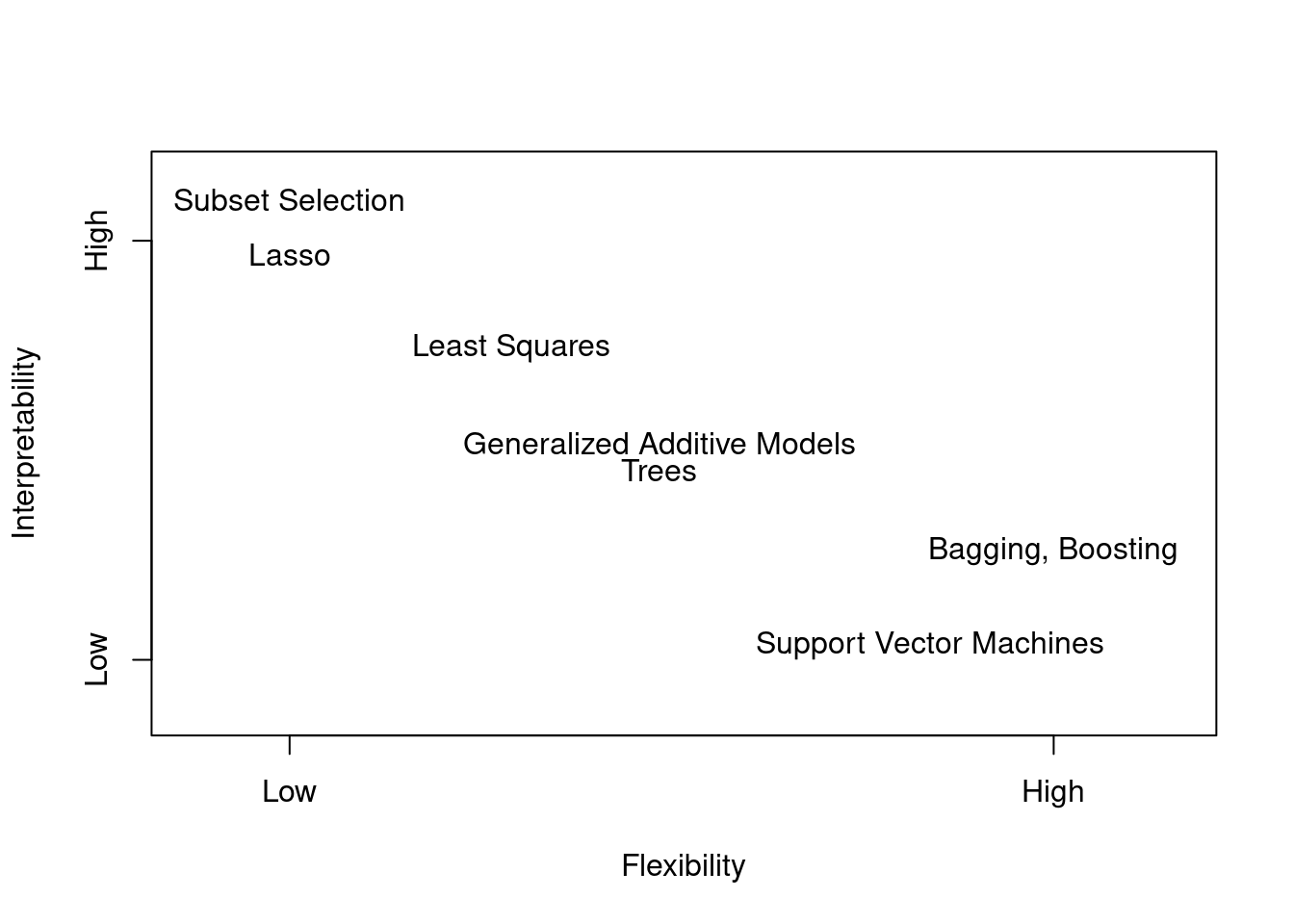

Method	Pro	Con
Linear Regression	Easy to interpret	Relatively inflexible
Thin Plate Splines	Very flexible	Difficult to understand
lasso	More interpretable	less flexible
GAMs	more flexible	less interpretable

2.1.4 2.1.4 Supervised Versus Unsupervised Learning

Most statistical learning problems fall into one of two categories: supervised or unsupervised.

Supervised Learning: For each observation of the predictor measurements \(X_i\), there is an associated response measurement \(Y_i\). These are models where we want to predict outcomes.

Unsupervised Learning: For each observation of the predictor measurements \(X_i\), there is No associated response measurement \(Y_i\)(!) - In this scenario, it is not possible to fit a linear regression, since there is no associated \(Y_i\).

2.1.4.1 Cluster Analysis

One way to understand unsupervised models is through cluster analysis. The goal of this type of analysis is to determine whether \(x_i, ..., x_n\) fall into relatively distinct groups.

Note:

Clustering methods are imprecise – They cannot assign all points to their correct group.
If there are \(p\) variables, then \(p(p- 1) /2)\) scatterplots can be made, this is why automated clustering methods are important.
There are instances where it is not clear whether a problem is supervised or unsupervised – Some \(Y\)’s exist, but not all. These are referred to as semi-supervised learning problems.

iris_cluster <- iris[, -5]
cls <- kmeans(x = iris_cluster, centers = 3)
iris_cluster$cluster <- as.character(cls$cluster)
ggplot() +
  geom_point(data = iris_cluster, 
             mapping = aes(x = Sepal.Length, 
                                  y = Petal.Length, 
                                  colour = cluster))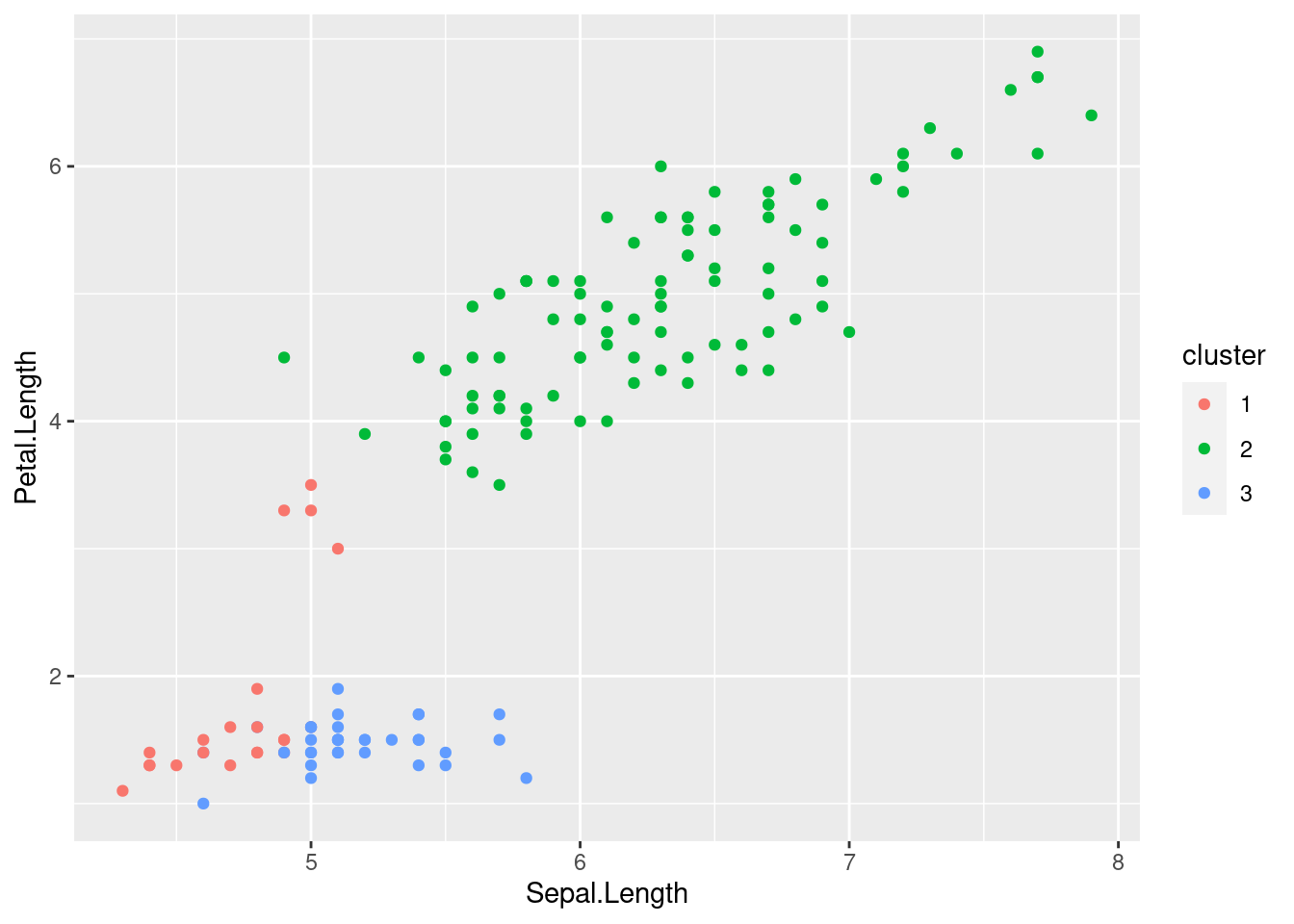

# borrowed from: https://rpubs.com/aephidayatuloh/clustervisual

2.1.5 2.1.5 Regression Versus Classification Problems

Problems with a quantitative response value (numeric) are referred to as regression problems.
Problems with a qualitative response – a value in one of \(K\) different classes, are referred to as classification problems.
Qualitative responses are also referred to as categorical values.

2.2 2.2 Assessing Model Accuracy

There is no free lunch in statistics: no one method dominates all others over all possible data sets. On a particular data set, one specific method may work best, but some other method may work better on a similar but different data set.

2.2.1 2.2.1 Measuring the Quality of Fit

When using regressions, quality of fit is most commonly assessed by mean squared error (MSE):

\[ MSE = \frac{1}{n}\sum_{i=1}^n(y_i - \hat{f}(x_i))^2 \] \(\hat{f}(x_i))^2\) is the prediction.

The training MSE will be small if the predicted responses are close to the true responses, and larger if the estimates of the predictions are farther from the true responses.

Examples:

If we are interested in stock prices based on the previous 6 months, we really only care about how well the algorithm predicts tomorrow’s price.
If we train a model on diabetes patient’s clinical measurements, we are only concerned with how well the model predicts future diabetes patients.

Mechanically: If we fit our method on training observations \({(x_1, y_1), (x_2, y_2), …, (x_n, y_n)}\), we use those observations to fit \(\hat{f}(x_1), \hat{f}(x_2), …, \hat{f}(x_n)\).

The aim here is to compute an \(\hat{f}(x_0)\) which is closest to the real unseen \(y_0\) observation, the test data.

2.2.1.1 How do we choose our model?

If we have test data available (not used for training/estimating \(\hat{f}\)), we can simply choose the method which minimizes \(MSE\) on that test data. If we do not have testing data, we can choose the model which minimizes \(MSE\) for our training data, but there is no guarantee that a method with the smallest training \(MSE\) will result in the smallest test \(MSE\).

Note: As model flexibility increases, the training \(MSE\) will decrease, but this does not imply that the test \(MSE\) will similarly decrease. When a method yields a small training \(MSE\) and a large test \(MSE\), we are overfitting our data.

2.2.2 2.2.2 The Bias-Variance Trade-Off

It is possible to prove that the expected test MSE can be decomposed into the sum of three quantities: the variance of \(\hat{f}(x_0)\), the squared bias of \(\hat{f}(x_0)\), and the variance of the error terms \(\epsilon\).

\[ E(y_0 - \hat{f}(x_0))^2 = Var(\hat{f}(x_0)) + [Bias(\hat{f}(x_0))]^2 + Var(\epsilon) \]

To achieve a low expected test error, it is necessary to select a method that results in low variance and low bias. It’s also important to understand that the MSE will never be lower than the \(Var(\epsilon)\), the irreducible error.

Variance refers to the amount \(\hat{f}\) would change if we used different testing data. Generally, more flexible models have higher variance.

Bias is the error introduced by using a simple model to approximate potentially complex functions. More flexible models generally have less bias.

The Bias-Variance trade-off is the challenge of identifying a model which has both low variance and low bias.

2.2.3 2.2.3 The Classification Setting

In the classification context, many of the concepts above still apply, with minor differences because the \(y_0\) is no longer a number value, but instead a qualitative value. The most common approach for gauging the accuracy of a qualitative \(\hat{f}\) is the training error rate:

\[ \frac 1 n \sum_{i=1}^n I(y_i \neq \hat{y_i}) \]

Where \(\hat{y_i}\) is the predicted value for the \(i\)th observation using the function \(\hat{f}\),

\(I(y_i \neq \hat{y_i})\) is an indicator variable, equal to 1 if \(y_i \neq \hat{y_i}\) and zero if not. This computes the fraction of incorrect classifications.

As with regression methods, the our aim should be to reduce the test error rate.

2.2.3.1 The Bayes Classifier

There is a special case in which it can be shown that the test error rate is minized by assigning each observation to it’s most likely class, based on it’s predictor values.

This case is called the Bayes Classifier

\[ Pr(Y = j | X = x_0) \]
This is the conditional probability that assigns a probability that \(Y = j\), given the observed value \(x_0\). In two class problems, this amounts to an assignment between two classes, class one if \(Pr(Y = 1 | X = x_0) > 0.5\), and class two otherwise. A scenario in which the decision boundary is set to exactly 50% is called a Bayes Decision Boundary.

The Bayes classifier always yields the lowest possible test error rate, since it will assign classification based on the highest probability outcome. The Bayes error rate is defined as:

\[ 1 - \mathrm{E} \lgroup \max_{j} \mathrm{ Pr}(Y=j|X) \] This error rate can also be described as the ratio of classifications that end up on the “wrong” side of the decision boundary.

2.2.3.2 K-Nearest Neighbors

For real data, we do not know the conditional distribution of \(Y\) given \(X\), so computing the Bayes classifier is impossible. One method is to estimate the distributionwith the highest estimated probability. One method is the K-Nearest Neighbors (KNN) approach.

The KNN classifier first identifies the \(K\) points closest to \(x_0\), represented by \(N_0\). It then estimates the probability for class \(j\) as a fraction of the observations in \(N_0\) whose response is equal to \(j\).

\[ Pr(Y=j|X=x_{0}) = \frac{1}{k} \sum_{i \in N_{0}} I (y_{i}=j) \] The KNN method then applies the Bayes rule and classifies \(x_0\) to the class with the highest probability.

The choice of \(K\) can have a drastic effect on the classification outcomes. Choosing a \(K\) that is too low will yield a too-flexible model, with high variance and low bias. Conversely, a \(K\) that is too high will result in a rigid classifier, with lower variance but higher bias.

2.3 2.3 Lab: Introduction to R

2.3.1 2.3.1 Basic Commands

To run a function called function, we type function(input). Objects are defined and then can be called by themselves.

# create a vector of numbers with the c() function
x <- c(1,3,2,5)
x

## [1] 1 3 2 5

print(x)

## [1] 1 3 2 5

We can check the length of an object in R using the length() function.

length(x) # 4

## [1] 4

The matrix() function can be used to create matrices of any size.

x <- matrix(data=c(1,2,3,4),nrow=2,ncol=2)
x

##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

The sqrt() function returns the square root of an object passed to it.

sqrt(x) # 4

##          [,1]     [,2]
## [1,] 1.000000 1.732051
## [2,] 1.414214 2.000000

The rnorm() function generates a vectors of random normal variables. We can use the cor() function to compute the correlation between two vectors.

x <- rnorm(50)
y = x * rnorm(5, mean = 50, sd = .1)

2.3.2 2.3.2 Graphics

plot() is the primary plotting function in base R. plot(x,y) will produce a plot with the vector x on the x-axis, and y on the y-axis.

plot(x, y)

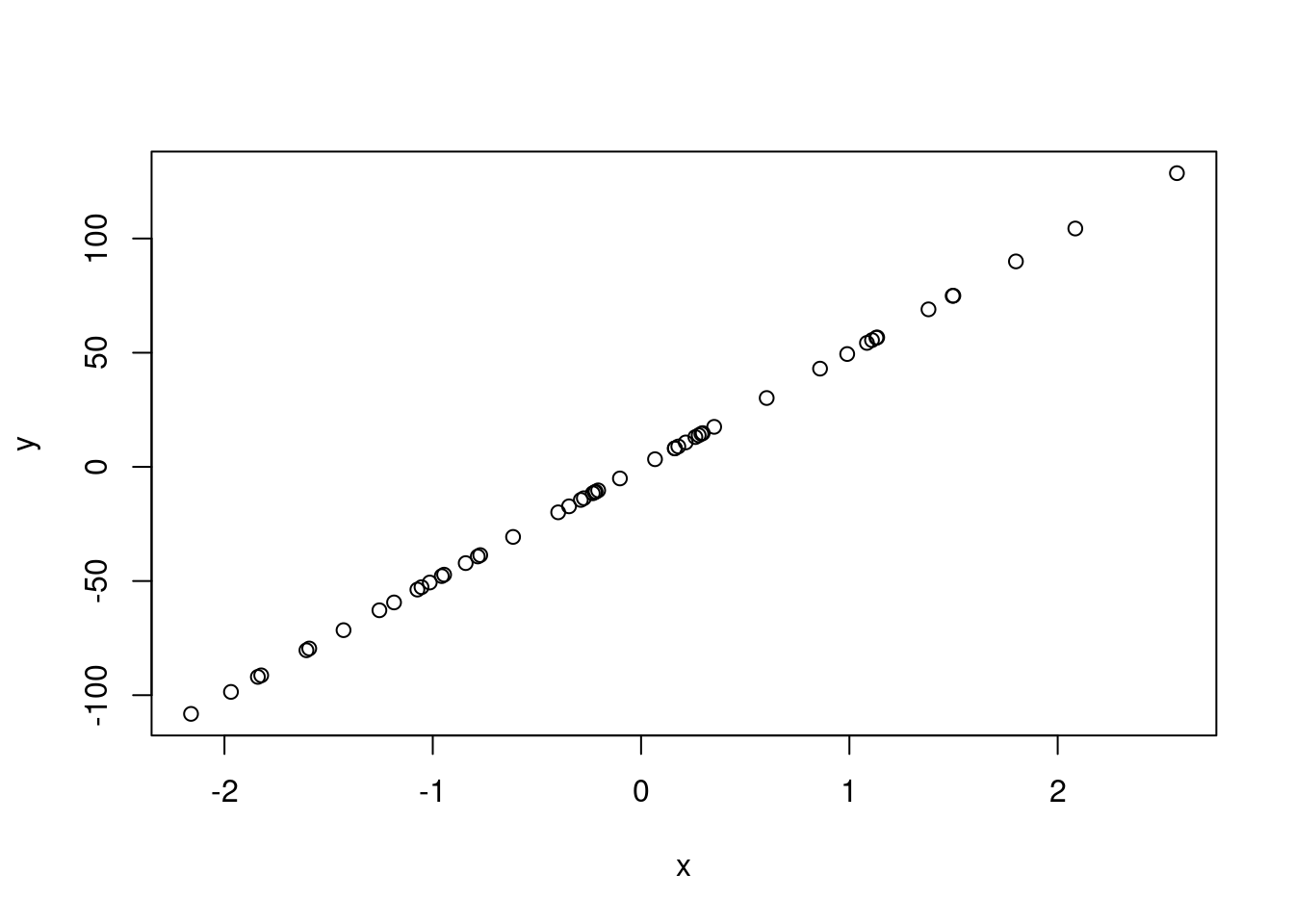Other useful functions:

mean()
var()
sqrt()
sd()
pdf()
jpeg()
dev.off()
seq()

x <- seq(1, 10)
y <- x
f <- outer(x, y, function(x, y) cos(y) / (1+x^2))
contour(x, y, f)

# contour(x, y, f, nlevels = 45, add = T)

2.3.3 2.3.3 Indexing Data

Indexing is useful for inspecting specific parts of whatever data we are working with.

A <- matrix(1:16,4,4)
A

##      [,1] [,2] [,3] [,4]
## [1,]    1    5    9   13
## [2,]    2    6   10   14
## [3,]    3    7   11   15
## [4,]    4    8   12   16

To access the third element of the second column:

A[2, 3] # Row 2, Column 3

## [1] 10

We can also access multiple rows or columns of data at once:

A[c(2:4), 3] # Rows 2 through 4, in Column 3

## [1] 10 11 12

2.3.4 2.3.4 Loading Data

To work with data in R, the first step is to load it into your session. The read.table() function can be used for this. There are lots of other functions you can use to read data into your session, including those from external packages.

Auto <- read.table("data/Auto.data")
head(Auto)

##     V1        V2           V3         V4     V5           V6   V7     V8
## 1  mpg cylinders displacement horsepower weight acceleration year origin
## 2 18.0         8        307.0      130.0  3504.         12.0   70      1
## 3 15.0         8        350.0      165.0  3693.         11.5   70      1
## 4 18.0         8        318.0      150.0  3436.         11.0   70      1
## 5 16.0         8        304.0      150.0  3433.         12.0   70      1
## 6 17.0         8        302.0      140.0  3449.         10.5   70      1
##                          V9
## 1                      name
## 2 chevrolet chevelle malibu
## 3         buick skylark 320
## 4        plymouth satellite
## 5             amc rebel sst
## 6               ford torino

2.3.4.1 Troubleshooting

It is a good idea to visually inspect your data before and after loading it into your R session. In this case, we have loaded the Auto.data incorrectly, and R assumes there are no column name values. To fix this:

Auto <- read.table("data/Auto.data", 
                   # argument for a header
                   header = T, 
                   # convert "?" strings to NA
                   na.strings = "?")

Other useful functions:
- na.omit() - dim()

2.3.5 2.3.5 Additional Graphical and Numerical Summaries

We can use the plot() function to create scatterplots of quantitative variables. When using this function, it is necessary to specify the dataset name:

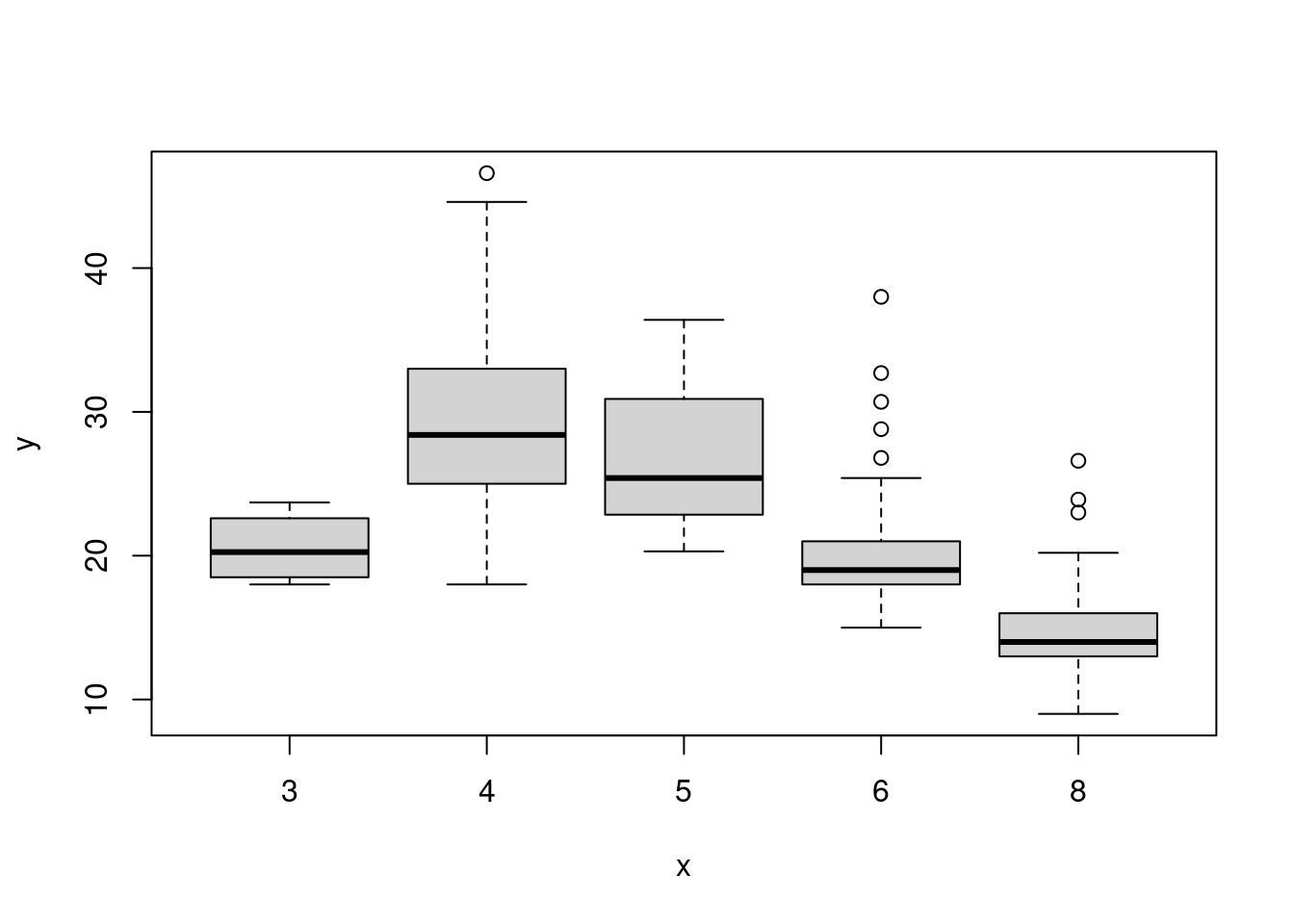
plot(x = as.factor(Auto$cylinders), y = Auto$mpg)

In the graph above, cylinder is converted in a factor variable, since there are only a specific number of possible values. If the variable on the \(x\)-axis is categorical, boxplots will automatically be drawn on the plot.

# There are many plot options available 
hist(Auto$mpg, col = "purple", 
     breaks = 15, 
     main = "Histogram of Miles per Gallon", xlab = "MPG")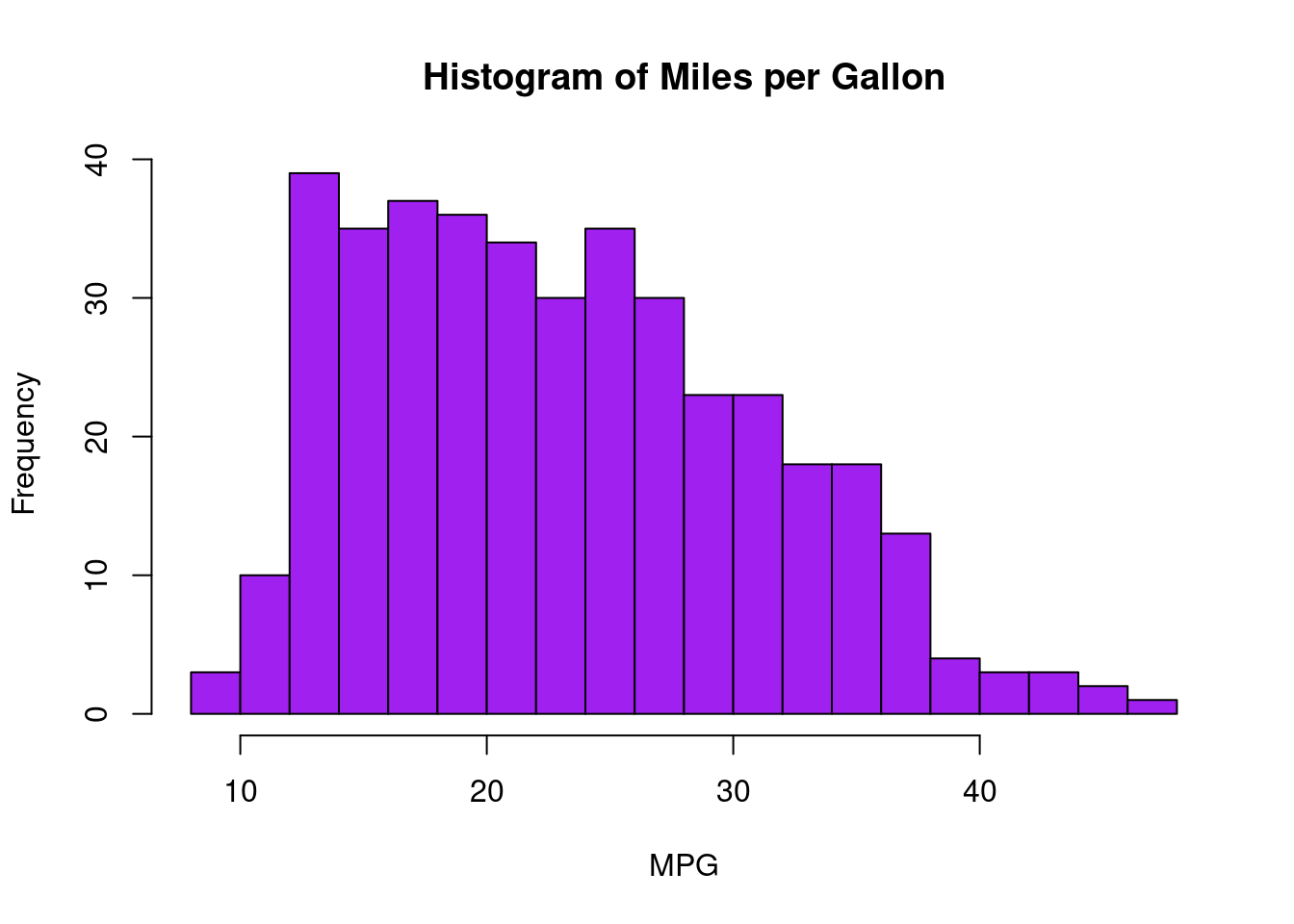

2.4 2.4 Exercises

2.4.1 Conceptual

2.4.1.1 1.

For each of parts (a) through (d), indicate whether we would generally expect the performance of a flexible statistical learning method to be better or worse than an inflexible method. Justify your answer.
(a) The sample size \(n\) is extremely large, and the number of predictors \(p\) is small.
> A flexible model would benefit from the large sample and would fit the data better.

The number of predictors \(p\) is extremely large, and the number of observations \(n\) is small.
> A flexible model would perform worse here and overfit because of the small \(n\).
The relationship between the predictors and response is highly non-linear.
> In this case, a more flexible model would perform better than an inflexible one.
The variance of the error terms, i.e. \(\sigma^2 = Var(\epsilon)\), is extremely high. > A flexible method would do worse in this situation, because it would fit to the noise in the error terms.

2.4.1.2 2.

Explain whether each scenario is a classification or regression problem, and indicate whether we are most interested in inference or prediction. Finally, provide \(n\) and \(p\).

We collect a set of data on the top 500 firms in the US. For each firm we record profit, number of employees, industry and the CEO salary. We are interested in understanding which factors affect CEO salary.
> Regression. \(n = 500\), \(p = 3\) – profit, employees, and industry.
We are considering launching a new product and wish to know whether it will be a success or a failure. We collect data on 20 similar products that were previously launched. For each product we have recorded whether it was a success or failure, price charged for the product, marketing budget, competition price, and ten other variables.
> Classification, the outcome variable will be either be ‘success’ or a ‘failure’. \(n = 20\), \(p = 13\) – price, marketing budget, competition price, and the 10 other variables.

2.4.1.3 3.

We now revisit the bias-variance decomposition.

Provide a sketch of typical (squared) bias, variance, training error, test error, and Bayes (or irreducible) error curves, on a single plot, as we go from less flexible statistical learning methods towards more flexible approaches. The x-axis should represent the amount of flexibility in the method, and the y-axis should represent the values for each curve. There should be five curves. Make sure to label each one.

An exercise left to the reader.

Explain why each of the five curves has the shape displayed in part (a).

The squared bias decreases monotonically as model flexibility increases. The variance increases monotonically as model flexibility increases. The training MSE declines as model flexibility increases. The test MSE initially declines, but begins to increase again as it starts to overfit. The irreducible error is constant at a level > 0.

2.4.1.4 4.

You will now think of some real-life applications for statistical learning.

Describe three real-life applications in which classification might be useful. Describe the response, as well as the predictors. Is the goal of each application inference or prediction? Explain your answer.

Mortgage Loan application approvals. Response: Loan Approval/Denial. Predictors: Credit score, income, location.
Disease detection. Response: Disease classification. Predictors: Health, genetic markers, sex.
Product success. Response: Whether a product is successful or not. Predictors: Competitor price, market share.

Describe three real-life applications in which regression might be useful. Describe the response, as well as the predictors. Is the goal of each application inference or prediction? Explain your answer.

Discuss!

Describe three real-life applications in which cluster analysis might be useful.

Discuss!

2.4.1.5 5.

What are the advantages and disadvantages of a very flexible (versus a less flexible) approach for regression or classification? Under what circumstances might a more flexible approach be preferred to a less flexible approach? When might a less flexible approach be preferred?

2.4.1.6 6.

Describe the differences between a parametric and a non-parametric statistical learning approach. What are the advantages of a parametric approach to regression or classification (as opposed to a non-parametric approach)? What are its disadvantages?

2.4.1.7 7.

The table below provides a training data set containing six observations, three predictors, and one qualitative response variable.

\(Obs\)	\(X_1\)	\(X_2\)	\(X_3\)	\(Y\)
\(1\)	\(0\)	\(3\)	\(0\)	\(Red\)
\(2\)	\(2\)	\(0\)	\(0\)	\(Red\)
\(3\)	\(0\)	\(1\)	\(3\)	\(Red\)
\(4\)	\(0\)	\(1\)	\(2\)	\(Green\)
\(5\)	\(-1\)	\(0\)	\(1\)	\(Green\)
\(6\)	\(1\)	\(1\)	\(1\)	\(Red\)

Suppose we wish to use this data set to make a prediction for Y when \(X_1 = X_2 = X_3 = 0\) using \(K\)-nearest neighbors.

Compute the Euclidean distance between each observation and the test point, \(X_1 = X_2 = X_3 = 0\).
What is our prediction with \(K = 1\)? Why?
What is our prediction with \(K = 3\)? Why?
If the Bayes decision boundary in this problem is highly non-linear, then would we expect the best value for \(K\) to be large or small? Why?

2.4.2 Applied

2.4.2.1 8.

This exercise relates to the College data set, which can be found in the file College.csv. It contains a number of variables for 777 different universities and colleges in the US. The variables are

Private: Public/private indicator
Apps: Number of applications received
Accept: Number of applicants accepted
Enroll: Number of new students enrolled
Top10perc: New students from top 10% of high school class
Top25perc: New students from top 25% of high school class
F.Undergrad: Number of full-time undergraduates
P.Undergrad: Number of part-time undergraduates
Outstate: Out-of-state tuition
Room.Board: Room and board costs
Books: Estimated book costs
Personal: Estimated personal spending
PhD:Percent of faculty with Ph.D.’s
Terminal:Percent of faculty with terminal degree
S.F.Ratio: Student/faculty ratio
perc.alumni: Percent of alumni who donate
Expend: Instructional expenditure per student
Grad.Rate: Graduation rate

Before reading the data into R, it can be viewed in Excel or a text editor.

Use the read.csv() function to read the data into R. Call the loaded data college. Make sure that you have the directory set to the correct location for the data.

if(!file.exists("data/Collage.csv")){
  download.file("https://www.statlearning.com/s/College.csv", destfile = "data/College.csv")
  }
college <- read.csv("data/College.csv")

Look at the data using the fix() function. You should notice that the first column is just the name of each university. We don’t really want R to treat this as data. However, it may be handy to have these names for later. Try the following commands:

# fix(college)
# add first column as rownames
rownames(college) <- college[, 1]
college <- college[, -1]

1. Use the summary() function to produce a numerical summary of the variables in the data set.

summary(college)

##    Private               Apps           Accept          Enroll    
##  Length:777         Min.   :   81   Min.   :   72   Min.   :  35  
##  Class :character   1st Qu.:  776   1st Qu.:  604   1st Qu.: 242  
##  Mode  :character   Median : 1558   Median : 1110   Median : 434  
##                     Mean   : 3002   Mean   : 2019   Mean   : 780  
##                     3rd Qu.: 3624   3rd Qu.: 2424   3rd Qu.: 902  
##                     Max.   :48094   Max.   :26330   Max.   :6392  
##    Top10perc       Top25perc      F.Undergrad     P.Undergrad     
##  Min.   : 1.00   Min.   :  9.0   Min.   :  139   Min.   :    1.0  
##  1st Qu.:15.00   1st Qu.: 41.0   1st Qu.:  992   1st Qu.:   95.0  
##  Median :23.00   Median : 54.0   Median : 1707   Median :  353.0  
##  Mean   :27.56   Mean   : 55.8   Mean   : 3700   Mean   :  855.3  
##  3rd Qu.:35.00   3rd Qu.: 69.0   3rd Qu.: 4005   3rd Qu.:  967.0  
##  Max.   :96.00   Max.   :100.0   Max.   :31643   Max.   :21836.0  
##     Outstate       Room.Board       Books           Personal   
##  Min.   : 2340   Min.   :1780   Min.   :  96.0   Min.   : 250  
##  1st Qu.: 7320   1st Qu.:3597   1st Qu.: 470.0   1st Qu.: 850  
##  Median : 9990   Median :4200   Median : 500.0   Median :1200  
##  Mean   :10441   Mean   :4358   Mean   : 549.4   Mean   :1341  
##  3rd Qu.:12925   3rd Qu.:5050   3rd Qu.: 600.0   3rd Qu.:1700  
##  Max.   :21700   Max.   :8124   Max.   :2340.0   Max.   :6800  
##       PhD            Terminal       S.F.Ratio      perc.alumni   
##  Min.   :  8.00   Min.   : 24.0   Min.   : 2.50   Min.   : 0.00  
##  1st Qu.: 62.00   1st Qu.: 71.0   1st Qu.:11.50   1st Qu.:13.00  
##  Median : 75.00   Median : 82.0   Median :13.60   Median :21.00  
##  Mean   : 72.66   Mean   : 79.7   Mean   :14.09   Mean   :22.74  
##  3rd Qu.: 85.00   3rd Qu.: 92.0   3rd Qu.:16.50   3rd Qu.:31.00  
##  Max.   :103.00   Max.   :100.0   Max.   :39.80   Max.   :64.00  
##      Expend        Grad.Rate     
##  Min.   : 3186   Min.   : 10.00  
##  1st Qu.: 6751   1st Qu.: 53.00  
##  Median : 8377   Median : 65.00  
##  Mean   : 9660   Mean   : 65.46  
##  3rd Qu.:10830   3rd Qu.: 78.00  
##  Max.   :56233   Max.   :118.00

1. Use the pairs() function to produce a scatterplot matrix of the first ten columns or variables of the data. Recall that you can reference the first ten columns of a matrix A using A[,1:10].

pairs(college[, 1:10])

## Error in pairs.default(college[, 1:10]): non-numeric argument to 'pairs'

1. Use the plot() function to produce side-by-side boxplots of Outstate versus Private.

plot(as.factor(college$Private), college$Outstate, xlab = "Private", ylab = "Out-of-state Tuition")

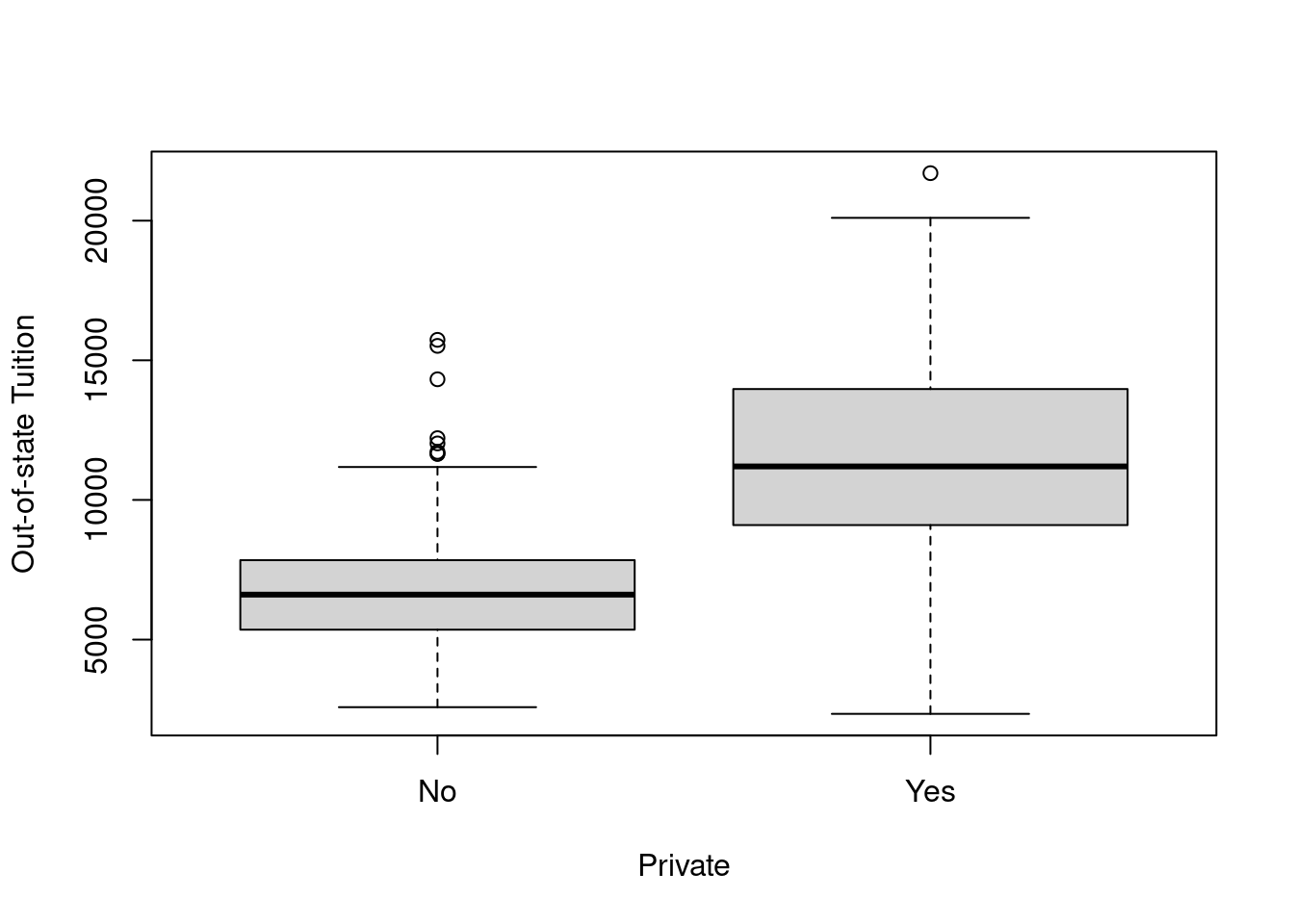
1. Create a new qualitative variable, called Elite, by binning the Top10perc variable. We are going to divide universitiesinto two groups based on whether or not the proportion of students coming from the top 10% of their high school classes exceeds 50%.

Elite <- rep("No",nrow(college))
Elite[college$Top10perc>50]="Yes" 
Elite <- as.factor(Elite)
college=data.frame(college,Elite)

Use the summary() function to see how many elite universities there are. Now use the plot() function to produce side-by-side boxplots of Outstate versus Elite.

summary(college$Elite)

##  No Yes 
## 699  78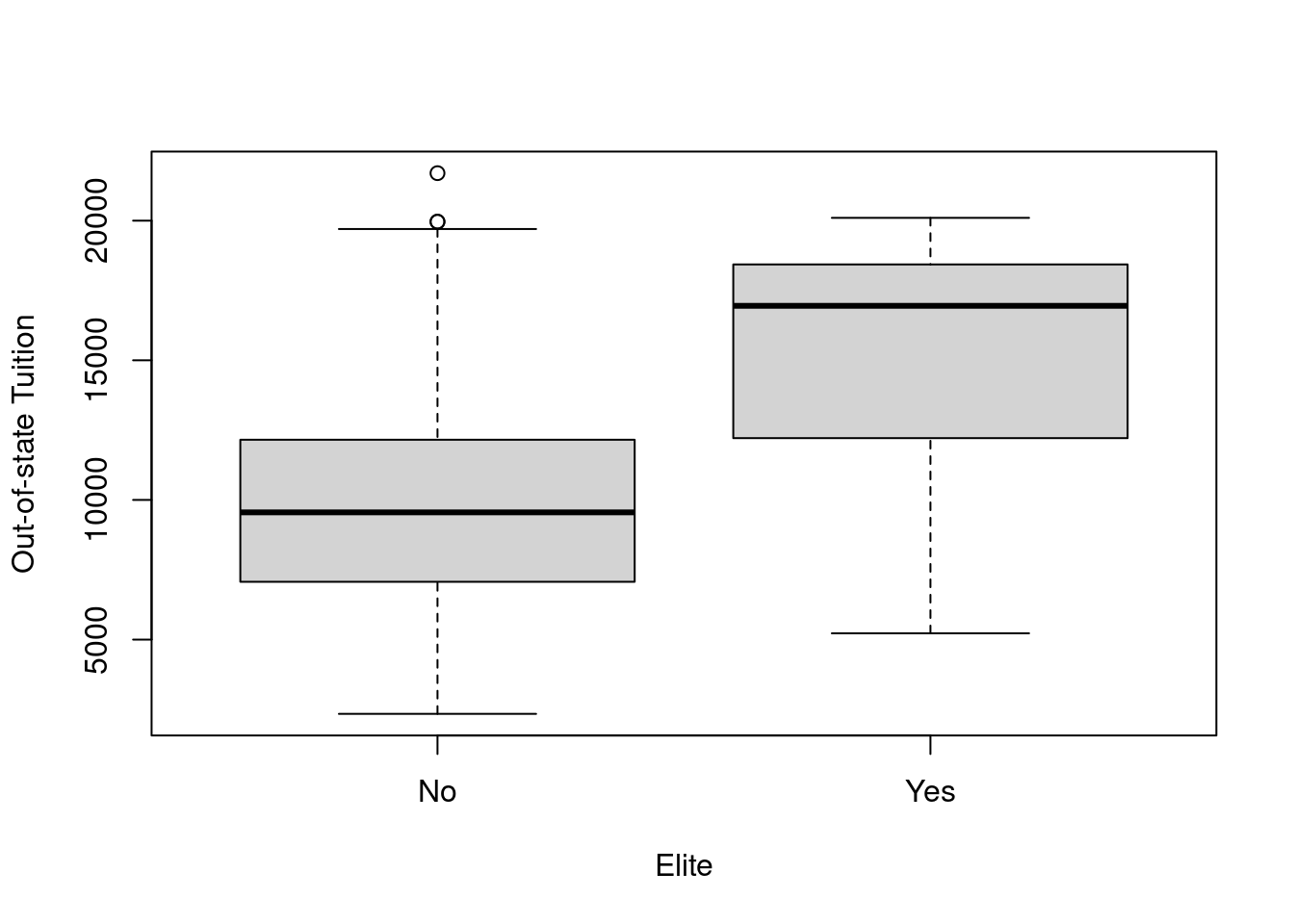

plot(as.factor(college$Elite), college$Outstate, xlab = "Elite", ylab = "Out-of-state Tuition")

1. Use the hist() function to produce some histograms with differing numbers of bins for a few of the quantitative variables. You may find the command par(mfrow=c(2,2)) useful: it will divide the print window into four regions so that four plots can be made simultaneously. Modifying the arguments to this function will divide the screen in other ways.

par(mfrow=c(2,2))
hist(college$Top10perc)
hist(college$F.Undergrad, breaks = 15)
hist(college$S.F.Ratio, breaks = 5)
hist(college$Room.Board, breaks = 10)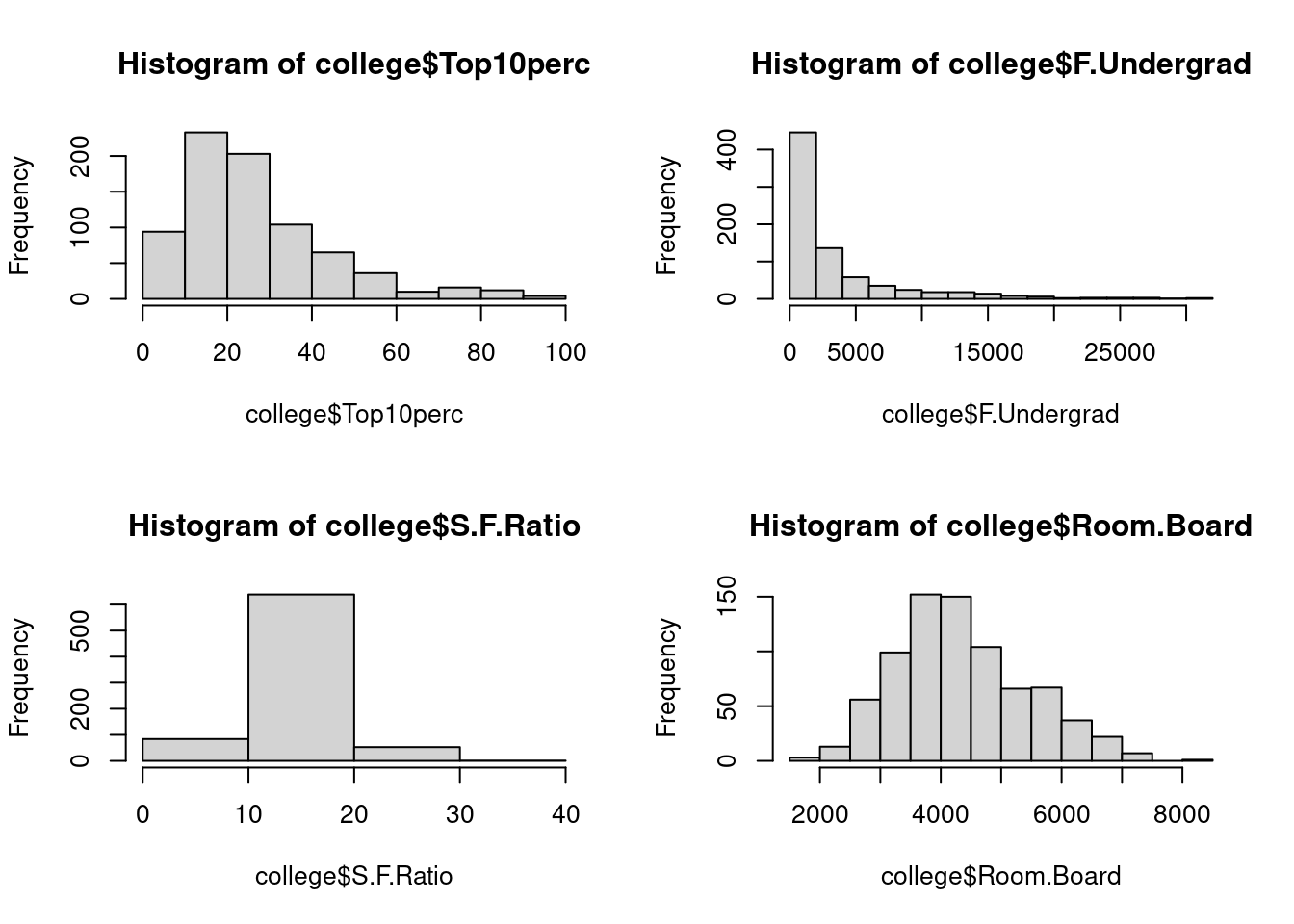

1. Continue exploring the data, and provide a brief summary of what you discover.

plot(college$S.F.Ratio, college$perc.alumni,
     xlab = "Student/Faculty Ratio", 
     ylab = "Percent of Alumni who Donate"
     )
lines(predict(lm(perc.alumni~S.F.Ratio, data = college)),
      col='red')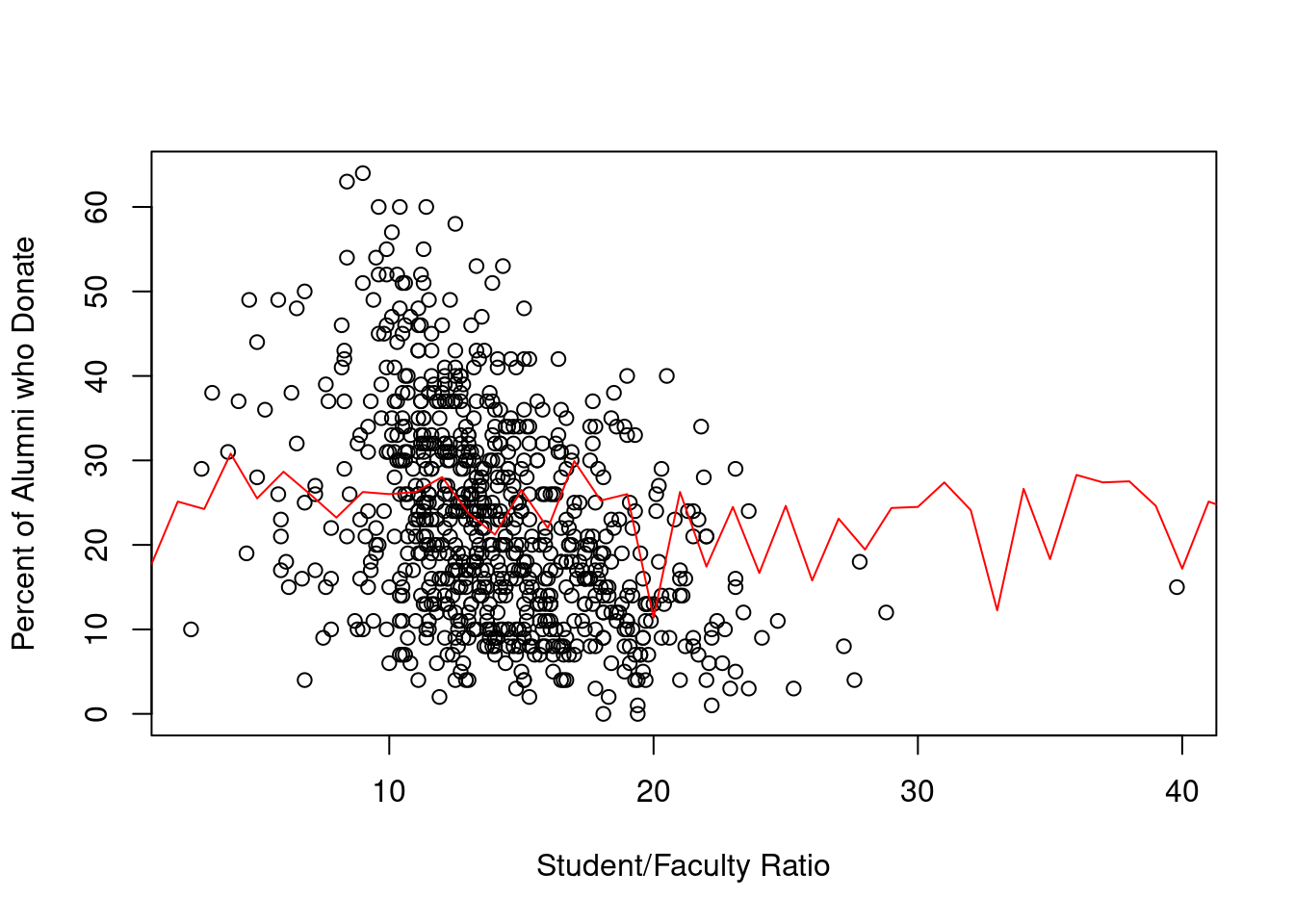

> Plotting Student/Faculty ratio and the percent of alumni who donate does not show clear relationship that I thought would show up. etc etc discuss.

2.4.2.2 9.

This exercise involves the Auto data set studied in the lab. Make sure that the missing values have been removed from the data.

Auto <- read.table("data/Auto.data", header = T, na.strings = "?")
Auto <- na.omit(Auto)
str(Auto)

## 'data.frame':    392 obs. of  9 variables:
##  $ mpg         : num  18 15 18 16 17 15 14 14 14 15 ...
##  $ cylinders   : int  8 8 8 8 8 8 8 8 8 8 ...
##  $ displacement: num  307 350 318 304 302 429 454 440 455 390 ...
##  $ horsepower  : num  130 165 150 150 140 198 220 215 225 190 ...
##  $ weight      : num  3504 3693 3436 3433 3449 ...
##  $ acceleration: num  12 11.5 11 12 10.5 10 9 8.5 10 8.5 ...
##  $ year        : int  70 70 70 70 70 70 70 70 70 70 ...
##  $ origin      : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ name        : chr  "chevrolet chevelle malibu" "buick skylark 320" "plymouth satellite" "amc rebel sst" ...
##  - attr(*, "na.action")= 'omit' Named int [1:5] 33 127 331 337 355
##   ..- attr(*, "names")= chr [1:5] "33" "127" "331" "337" ...

Which of the predictors are quantitative, and which are qualitative?

Cylinders, origin, and name are the qualitative variables. The rest of the variables are quantitative.

What is the range of each quantitative predictor? You can answer this using the range() function.

# this is a fancy way to do this
vars <- setdiff(names(Auto), c("cylinders", "origin", "name"))
sapply(vars, function(v) range(Auto[v]), USE.NAMES = T)

##       mpg displacement horsepower weight acceleration year
## [1,]  9.0           68         46   1613          8.0   70
## [2,] 46.6          455        230   5140         24.8   82

What is the mean and standard deviation of each quantitative predictor?

sapply(Auto[, vars], mean, USE.NAMES = T)

##          mpg displacement   horsepower       weight acceleration         year 
##     23.44592    194.41199    104.46939   2977.58418     15.54133     75.97959

sapply(Auto[, vars], sd, USE.NAMES = T)

##          mpg displacement   horsepower       weight acceleration         year 
##     7.805007   104.644004    38.491160   849.402560     2.758864     3.683737

Now remove the 10th through 85th observations. What is the range, mean, and standard deviation of each predictor in the subset of the data that remains?

new_auto <- Auto[-c(10:85)]

sapply(new_auto[, vars], range, USE.NAMES = T)

##       mpg displacement horsepower weight acceleration year
## [1,]  9.0           68         46   1613          8.0   70
## [2,] 46.6          455        230   5140         24.8   82

sapply(new_auto[, vars], mean, USE.NAMES = T)

##          mpg displacement   horsepower       weight acceleration         year 
##     23.44592    194.41199    104.46939   2977.58418     15.54133     75.97959

sapply(new_auto[, vars], sd, USE.NAMES = T)

##          mpg displacement   horsepower       weight acceleration         year 
##     7.805007   104.644004    38.491160   849.402560     2.758864     3.683737

Using the full data set, investigate the predictors graphically, using scatterplots or other tools of your choice. Create some plots highlighting the relationships among the predictors. Comment on your findings.

pairs(Auto)

## Error in pairs.default(Auto): non-numeric argument to 'pairs'

Suppose that we wish to predict gas mileage ( mpg ) on the basis of the other variables. Do your plots suggest that any of the other variables might be useful in predicting mpg ? Justify your answer.

cor(Auto$weight, Auto$horsepower)

## [1] 0.8645377

cor(Auto$weight, Auto$displacement)

## [1] 0.9329944

2.4.2.3 10.

This exercise involves the Boston housing data set.

To begin, load in the Boston data set. The Boston data set is part of the MASS library in R.

library(MASS)

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

Boston

##         crim    zn indus chas    nox    rm   age     dis rad tax ptratio  black
## 1    0.00632  18.0  2.31    0 0.5380 6.575  65.2  4.0900   1 296    15.3 396.90
## 2    0.02731   0.0  7.07    0 0.4690 6.421  78.9  4.9671   2 242    17.8 396.90
## 3    0.02729   0.0  7.07    0 0.4690 7.185  61.1  4.9671   2 242    17.8 392.83
## 4    0.03237   0.0  2.18    0 0.4580 6.998  45.8  6.0622   3 222    18.7 394.63
## 5    0.06905   0.0  2.18    0 0.4580 7.147  54.2  6.0622   3 222    18.7 396.90
## 6    0.02985   0.0  2.18    0 0.4580 6.430  58.7  6.0622   3 222    18.7 394.12
## 7    0.08829  12.5  7.87    0 0.5240 6.012  66.6  5.5605   5 311    15.2 395.60
## 8    0.14455  12.5  7.87    0 0.5240 6.172  96.1  5.9505   5 311    15.2 396.90
## 9    0.21124  12.5  7.87    0 0.5240 5.631 100.0  6.0821   5 311    15.2 386.63
## 10   0.17004  12.5  7.87    0 0.5240 6.004  85.9  6.5921   5 311    15.2 386.71
## 11   0.22489  12.5  7.87    0 0.5240 6.377  94.3  6.3467   5 311    15.2 392.52
## 12   0.11747  12.5  7.87    0 0.5240 6.009  82.9  6.2267   5 311    15.2 396.90
## 13   0.09378  12.5  7.87    0 0.5240 5.889  39.0  5.4509   5 311    15.2 390.50
## 14   0.62976   0.0  8.14    0 0.5380 5.949  61.8  4.7075   4 307    21.0 396.90
## 15   0.63796   0.0  8.14    0 0.5380 6.096  84.5  4.4619   4 307    21.0 380.02
## 16   0.62739   0.0  8.14    0 0.5380 5.834  56.5  4.4986   4 307    21.0 395.62
## 17   1.05393   0.0  8.14    0 0.5380 5.935  29.3  4.4986   4 307    21.0 386.85
## 18   0.78420   0.0  8.14    0 0.5380 5.990  81.7  4.2579   4 307    21.0 386.75
## 19   0.80271   0.0  8.14    0 0.5380 5.456  36.6  3.7965   4 307    21.0 288.99
## 20   0.72580   0.0  8.14    0 0.5380 5.727  69.5  3.7965   4 307    21.0 390.95
## 21   1.25179   0.0  8.14    0 0.5380 5.570  98.1  3.7979   4 307    21.0 376.57
## 22   0.85204   0.0  8.14    0 0.5380 5.965  89.2  4.0123   4 307    21.0 392.53
## 23   1.23247   0.0  8.14    0 0.5380 6.142  91.7  3.9769   4 307    21.0 396.90
## 24   0.98843   0.0  8.14    0 0.5380 5.813 100.0  4.0952   4 307    21.0 394.54
## 25   0.75026   0.0  8.14    0 0.5380 5.924  94.1  4.3996   4 307    21.0 394.33
## 26   0.84054   0.0  8.14    0 0.5380 5.599  85.7  4.4546   4 307    21.0 303.42
## 27   0.67191   0.0  8.14    0 0.5380 5.813  90.3  4.6820   4 307    21.0 376.88
## 28   0.95577   0.0  8.14    0 0.5380 6.047  88.8  4.4534   4 307    21.0 306.38
## 29   0.77299   0.0  8.14    0 0.5380 6.495  94.4  4.4547   4 307    21.0 387.94
## 30   1.00245   0.0  8.14    0 0.5380 6.674  87.3  4.2390   4 307    21.0 380.23
## 31   1.13081   0.0  8.14    0 0.5380 5.713  94.1  4.2330   4 307    21.0 360.17
## 32   1.35472   0.0  8.14    0 0.5380 6.072 100.0  4.1750   4 307    21.0 376.73
## 33   1.38799   0.0  8.14    0 0.5380 5.950  82.0  3.9900   4 307    21.0 232.60
## 34   1.15172   0.0  8.14    0 0.5380 5.701  95.0  3.7872   4 307    21.0 358.77
## 35   1.61282   0.0  8.14    0 0.5380 6.096  96.9  3.7598   4 307    21.0 248.31
## 36   0.06417   0.0  5.96    0 0.4990 5.933  68.2  3.3603   5 279    19.2 396.90
## 37   0.09744   0.0  5.96    0 0.4990 5.841  61.4  3.3779   5 279    19.2 377.56
## 38   0.08014   0.0  5.96    0 0.4990 5.850  41.5  3.9342   5 279    19.2 396.90
## 39   0.17505   0.0  5.96    0 0.4990 5.966  30.2  3.8473   5 279    19.2 393.43
## 40   0.02763  75.0  2.95    0 0.4280 6.595  21.8  5.4011   3 252    18.3 395.63
## 41   0.03359  75.0  2.95    0 0.4280 7.024  15.8  5.4011   3 252    18.3 395.62
## 42   0.12744   0.0  6.91    0 0.4480 6.770   2.9  5.7209   3 233    17.9 385.41
## 43   0.14150   0.0  6.91    0 0.4480 6.169   6.6  5.7209   3 233    17.9 383.37
## 44   0.15936   0.0  6.91    0 0.4480 6.211   6.5  5.7209   3 233    17.9 394.46
## 45   0.12269   0.0  6.91    0 0.4480 6.069  40.0  5.7209   3 233    17.9 389.39
## 46   0.17142   0.0  6.91    0 0.4480 5.682  33.8  5.1004   3 233    17.9 396.90
## 47   0.18836   0.0  6.91    0 0.4480 5.786  33.3  5.1004   3 233    17.9 396.90
## 48   0.22927   0.0  6.91    0 0.4480 6.030  85.5  5.6894   3 233    17.9 392.74
## 49   0.25387   0.0  6.91    0 0.4480 5.399  95.3  5.8700   3 233    17.9 396.90
## 50   0.21977   0.0  6.91    0 0.4480 5.602  62.0  6.0877   3 233    17.9 396.90
## 51   0.08873  21.0  5.64    0 0.4390 5.963  45.7  6.8147   4 243    16.8 395.56
## 52   0.04337  21.0  5.64    0 0.4390 6.115  63.0  6.8147   4 243    16.8 393.97
## 53   0.05360  21.0  5.64    0 0.4390 6.511  21.1  6.8147   4 243    16.8 396.90
## 54   0.04981  21.0  5.64    0 0.4390 5.998  21.4  6.8147   4 243    16.8 396.90
## 55   0.01360  75.0  4.00    0 0.4100 5.888  47.6  7.3197   3 469    21.1 396.90
## 56   0.01311  90.0  1.22    0 0.4030 7.249  21.9  8.6966   5 226    17.9 395.93
## 57   0.02055  85.0  0.74    0 0.4100 6.383  35.7  9.1876   2 313    17.3 396.90
## 58   0.01432 100.0  1.32    0 0.4110 6.816  40.5  8.3248   5 256    15.1 392.90
## 59   0.15445  25.0  5.13    0 0.4530 6.145  29.2  7.8148   8 284    19.7 390.68
## 60   0.10328  25.0  5.13    0 0.4530 5.927  47.2  6.9320   8 284    19.7 396.90
## 61   0.14932  25.0  5.13    0 0.4530 5.741  66.2  7.2254   8 284    19.7 395.11
## 62   0.17171  25.0  5.13    0 0.4530 5.966  93.4  6.8185   8 284    19.7 378.08
## 63   0.11027  25.0  5.13    0 0.4530 6.456  67.8  7.2255   8 284    19.7 396.90
## 64   0.12650  25.0  5.13    0 0.4530 6.762  43.4  7.9809   8 284    19.7 395.58
## 65   0.01951  17.5  1.38    0 0.4161 7.104  59.5  9.2229   3 216    18.6 393.24
## 66   0.03584  80.0  3.37    0 0.3980 6.290  17.8  6.6115   4 337    16.1 396.90
## 67   0.04379  80.0  3.37    0 0.3980 5.787  31.1  6.6115   4 337    16.1 396.90
## 68   0.05789  12.5  6.07    0 0.4090 5.878  21.4  6.4980   4 345    18.9 396.21
## 69   0.13554  12.5  6.07    0 0.4090 5.594  36.8  6.4980   4 345    18.9 396.90
## 70   0.12816  12.5  6.07    0 0.4090 5.885  33.0  6.4980   4 345    18.9 396.90
## 71   0.08826   0.0 10.81    0 0.4130 6.417   6.6  5.2873   4 305    19.2 383.73
## 72   0.15876   0.0 10.81    0 0.4130 5.961  17.5  5.2873   4 305    19.2 376.94
## 73   0.09164   0.0 10.81    0 0.4130 6.065   7.8  5.2873   4 305    19.2 390.91
## 74   0.19539   0.0 10.81    0 0.4130 6.245   6.2  5.2873   4 305    19.2 377.17
## 75   0.07896   0.0 12.83    0 0.4370 6.273   6.0  4.2515   5 398    18.7 394.92
## 76   0.09512   0.0 12.83    0 0.4370 6.286  45.0  4.5026   5 398    18.7 383.23
## 77   0.10153   0.0 12.83    0 0.4370 6.279  74.5  4.0522   5 398    18.7 373.66
## 78   0.08707   0.0 12.83    0 0.4370 6.140  45.8  4.0905   5 398    18.7 386.96
## 79   0.05646   0.0 12.83    0 0.4370 6.232  53.7  5.0141   5 398    18.7 386.40
## 80   0.08387   0.0 12.83    0 0.4370 5.874  36.6  4.5026   5 398    18.7 396.06
## 81   0.04113  25.0  4.86    0 0.4260 6.727  33.5  5.4007   4 281    19.0 396.90
## 82   0.04462  25.0  4.86    0 0.4260 6.619  70.4  5.4007   4 281    19.0 395.63
## 83   0.03659  25.0  4.86    0 0.4260 6.302  32.2  5.4007   4 281    19.0 396.90
## 84   0.03551  25.0  4.86    0 0.4260 6.167  46.7  5.4007   4 281    19.0 390.64
## 85   0.05059   0.0  4.49    0 0.4490 6.389  48.0  4.7794   3 247    18.5 396.90
## 86   0.05735   0.0  4.49    0 0.4490 6.630  56.1  4.4377   3 247    18.5 392.30
## 87   0.05188   0.0  4.49    0 0.4490 6.015  45.1  4.4272   3 247    18.5 395.99
## 88   0.07151   0.0  4.49    0 0.4490 6.121  56.8  3.7476   3 247    18.5 395.15
## 89   0.05660   0.0  3.41    0 0.4890 7.007  86.3  3.4217   2 270    17.8 396.90
## 90   0.05302   0.0  3.41    0 0.4890 7.079  63.1  3.4145   2 270    17.8 396.06
## 91   0.04684   0.0  3.41    0 0.4890 6.417  66.1  3.0923   2 270    17.8 392.18
## 92   0.03932   0.0  3.41    0 0.4890 6.405  73.9  3.0921   2 270    17.8 393.55
## 93   0.04203  28.0 15.04    0 0.4640 6.442  53.6  3.6659   4 270    18.2 395.01
## 94   0.02875  28.0 15.04    0 0.4640 6.211  28.9  3.6659   4 270    18.2 396.33
## 95   0.04294  28.0 15.04    0 0.4640 6.249  77.3  3.6150   4 270    18.2 396.90
## 96   0.12204   0.0  2.89    0 0.4450 6.625  57.8  3.4952   2 276    18.0 357.98
## 97   0.11504   0.0  2.89    0 0.4450 6.163  69.6  3.4952   2 276    18.0 391.83
## 98   0.12083   0.0  2.89    0 0.4450 8.069  76.0  3.4952   2 276    18.0 396.90
## 99   0.08187   0.0  2.89    0 0.4450 7.820  36.9  3.4952   2 276    18.0 393.53
## 100  0.06860   0.0  2.89    0 0.4450 7.416  62.5  3.4952   2 276    18.0 396.90
## 101  0.14866   0.0  8.56    0 0.5200 6.727  79.9  2.7778   5 384    20.9 394.76
## 102  0.11432   0.0  8.56    0 0.5200 6.781  71.3  2.8561   5 384    20.9 395.58
## 103  0.22876   0.0  8.56    0 0.5200 6.405  85.4  2.7147   5 384    20.9  70.80
## 104  0.21161   0.0  8.56    0 0.5200 6.137  87.4  2.7147   5 384    20.9 394.47
## 105  0.13960   0.0  8.56    0 0.5200 6.167  90.0  2.4210   5 384    20.9 392.69
## 106  0.13262   0.0  8.56    0 0.5200 5.851  96.7  2.1069   5 384    20.9 394.05
## 107  0.17120   0.0  8.56    0 0.5200 5.836  91.9  2.2110   5 384    20.9 395.67
## 108  0.13117   0.0  8.56    0 0.5200 6.127  85.2  2.1224   5 384    20.9 387.69
## 109  0.12802   0.0  8.56    0 0.5200 6.474  97.1  2.4329   5 384    20.9 395.24
## 110  0.26363   0.0  8.56    0 0.5200 6.229  91.2  2.5451   5 384    20.9 391.23
## 111  0.10793   0.0  8.56    0 0.5200 6.195  54.4  2.7778   5 384    20.9 393.49
## 112  0.10084   0.0 10.01    0 0.5470 6.715  81.6  2.6775   6 432    17.8 395.59
## 113  0.12329   0.0 10.01    0 0.5470 5.913  92.9  2.3534   6 432    17.8 394.95
## 114  0.22212   0.0 10.01    0 0.5470 6.092  95.4  2.5480   6 432    17.8 396.90
## 115  0.14231   0.0 10.01    0 0.5470 6.254  84.2  2.2565   6 432    17.8 388.74
## 116  0.17134   0.0 10.01    0 0.5470 5.928  88.2  2.4631   6 432    17.8 344.91
## 117  0.13158   0.0 10.01    0 0.5470 6.176  72.5  2.7301   6 432    17.8 393.30
## 118  0.15098   0.0 10.01    0 0.5470 6.021  82.6  2.7474   6 432    17.8 394.51
## 119  0.13058   0.0 10.01    0 0.5470 5.872  73.1  2.4775   6 432    17.8 338.63
## 120  0.14476   0.0 10.01    0 0.5470 5.731  65.2  2.7592   6 432    17.8 391.50
## 121  0.06899   0.0 25.65    0 0.5810 5.870  69.7  2.2577   2 188    19.1 389.15
## 122  0.07165   0.0 25.65    0 0.5810 6.004  84.1  2.1974   2 188    19.1 377.67
## 123  0.09299   0.0 25.65    0 0.5810 5.961  92.9  2.0869   2 188    19.1 378.09
## 124  0.15038   0.0 25.65    0 0.5810 5.856  97.0  1.9444   2 188    19.1 370.31
## 125  0.09849   0.0 25.65    0 0.5810 5.879  95.8  2.0063   2 188    19.1 379.38
## 126  0.16902   0.0 25.65    0 0.5810 5.986  88.4  1.9929   2 188    19.1 385.02
## 127  0.38735   0.0 25.65    0 0.5810 5.613  95.6  1.7572   2 188    19.1 359.29
## 128  0.25915   0.0 21.89    0 0.6240 5.693  96.0  1.7883   4 437    21.2 392.11
## 129  0.32543   0.0 21.89    0 0.6240 6.431  98.8  1.8125   4 437    21.2 396.90
## 130  0.88125   0.0 21.89    0 0.6240 5.637  94.7  1.9799   4 437    21.2 396.90
## 131  0.34006   0.0 21.89    0 0.6240 6.458  98.9  2.1185   4 437    21.2 395.04
## 132  1.19294   0.0 21.89    0 0.6240 6.326  97.7  2.2710   4 437    21.2 396.90
## 133  0.59005   0.0 21.89    0 0.6240 6.372  97.9  2.3274   4 437    21.2 385.76
## 134  0.32982   0.0 21.89    0 0.6240 5.822  95.4  2.4699   4 437    21.2 388.69
## 135  0.97617   0.0 21.89    0 0.6240 5.757  98.4  2.3460   4 437    21.2 262.76
## 136  0.55778   0.0 21.89    0 0.6240 6.335  98.2  2.1107   4 437    21.2 394.67
## 137  0.32264   0.0 21.89    0 0.6240 5.942  93.5  1.9669   4 437    21.2 378.25
## 138  0.35233   0.0 21.89    0 0.6240 6.454  98.4  1.8498   4 437    21.2 394.08
## 139  0.24980   0.0 21.89    0 0.6240 5.857  98.2  1.6686   4 437    21.2 392.04
## 140  0.54452   0.0 21.89    0 0.6240 6.151  97.9  1.6687   4 437    21.2 396.90
## 141  0.29090   0.0 21.89    0 0.6240 6.174  93.6  1.6119   4 437    21.2 388.08
## 142  1.62864   0.0 21.89    0 0.6240 5.019 100.0  1.4394   4 437    21.2 396.90
## 143  3.32105   0.0 19.58    1 0.8710 5.403 100.0  1.3216   5 403    14.7 396.90
## 144  4.09740   0.0 19.58    0 0.8710 5.468 100.0  1.4118   5 403    14.7 396.90
## 145  2.77974   0.0 19.58    0 0.8710 4.903  97.8  1.3459   5 403    14.7 396.90
## 146  2.37934   0.0 19.58    0 0.8710 6.130 100.0  1.4191   5 403    14.7 172.91
## 147  2.15505   0.0 19.58    0 0.8710 5.628 100.0  1.5166   5 403    14.7 169.27
## 148  2.36862   0.0 19.58    0 0.8710 4.926  95.7  1.4608   5 403    14.7 391.71
## 149  2.33099   0.0 19.58    0 0.8710 5.186  93.8  1.5296   5 403    14.7 356.99
## 150  2.73397   0.0 19.58    0 0.8710 5.597  94.9  1.5257   5 403    14.7 351.85
## 151  1.65660   0.0 19.58    0 0.8710 6.122  97.3  1.6180   5 403    14.7 372.80
## 152  1.49632   0.0 19.58    0 0.8710 5.404 100.0  1.5916   5 403    14.7 341.60
## 153  1.12658   0.0 19.58    1 0.8710 5.012  88.0  1.6102   5 403    14.7 343.28
## 154  2.14918   0.0 19.58    0 0.8710 5.709  98.5  1.6232   5 403    14.7 261.95
## 155  1.41385   0.0 19.58    1 0.8710 6.129  96.0  1.7494   5 403    14.7 321.02
## 156  3.53501   0.0 19.58    1 0.8710 6.152  82.6  1.7455   5 403    14.7  88.01
## 157  2.44668   0.0 19.58    0 0.8710 5.272  94.0  1.7364   5 403    14.7  88.63
## 158  1.22358   0.0 19.58    0 0.6050 6.943  97.4  1.8773   5 403    14.7 363.43
## 159  1.34284   0.0 19.58    0 0.6050 6.066 100.0  1.7573   5 403    14.7 353.89
## 160  1.42502   0.0 19.58    0 0.8710 6.510 100.0  1.7659   5 403    14.7 364.31
## 161  1.27346   0.0 19.58    1 0.6050 6.250  92.6  1.7984   5 403    14.7 338.92
## 162  1.46336   0.0 19.58    0 0.6050 7.489  90.8  1.9709   5 403    14.7 374.43
## 163  1.83377   0.0 19.58    1 0.6050 7.802  98.2  2.0407   5 403    14.7 389.61
## 164  1.51902   0.0 19.58    1 0.6050 8.375  93.9  2.1620   5 403    14.7 388.45
## 165  2.24236   0.0 19.58    0 0.6050 5.854  91.8  2.4220   5 403    14.7 395.11
## 166  2.92400   0.0 19.58    0 0.6050 6.101  93.0  2.2834   5 403    14.7 240.16
## 167  2.01019   0.0 19.58    0 0.6050 7.929  96.2  2.0459   5 403    14.7 369.30
## 168  1.80028   0.0 19.58    0 0.6050 5.877  79.2  2.4259   5 403    14.7 227.61
## 169  2.30040   0.0 19.58    0 0.6050 6.319  96.1  2.1000   5 403    14.7 297.09
## 170  2.44953   0.0 19.58    0 0.6050 6.402  95.2  2.2625   5 403    14.7 330.04
## 171  1.20742   0.0 19.58    0 0.6050 5.875  94.6  2.4259   5 403    14.7 292.29
## 172  2.31390   0.0 19.58    0 0.6050 5.880  97.3  2.3887   5 403    14.7 348.13
## 173  0.13914   0.0  4.05    0 0.5100 5.572  88.5  2.5961   5 296    16.6 396.90
## 174  0.09178   0.0  4.05    0 0.5100 6.416  84.1  2.6463   5 296    16.6 395.50
## 175  0.08447   0.0  4.05    0 0.5100 5.859  68.7  2.7019   5 296    16.6 393.23
## 176  0.06664   0.0  4.05    0 0.5100 6.546  33.1  3.1323   5 296    16.6 390.96
## 177  0.07022   0.0  4.05    0 0.5100 6.020  47.2  3.5549   5 296    16.6 393.23
## 178  0.05425   0.0  4.05    0 0.5100 6.315  73.4  3.3175   5 296    16.6 395.60
## 179  0.06642   0.0  4.05    0 0.5100 6.860  74.4  2.9153   5 296    16.6 391.27
## 180  0.05780   0.0  2.46    0 0.4880 6.980  58.4  2.8290   3 193    17.8 396.90
## 181  0.06588   0.0  2.46    0 0.4880 7.765  83.3  2.7410   3 193    17.8 395.56
## 182  0.06888   0.0  2.46    0 0.4880 6.144  62.2  2.5979   3 193    17.8 396.90
## 183  0.09103   0.0  2.46    0 0.4880 7.155  92.2  2.7006   3 193    17.8 394.12
## 184  0.10008   0.0  2.46    0 0.4880 6.563  95.6  2.8470   3 193    17.8 396.90
## 185  0.08308   0.0  2.46    0 0.4880 5.604  89.8  2.9879   3 193    17.8 391.00
## 186  0.06047   0.0  2.46    0 0.4880 6.153  68.8  3.2797   3 193    17.8 387.11
## 187  0.05602   0.0  2.46    0 0.4880 7.831  53.6  3.1992   3 193    17.8 392.63
## 188  0.07875  45.0  3.44    0 0.4370 6.782  41.1  3.7886   5 398    15.2 393.87
## 189  0.12579  45.0  3.44    0 0.4370 6.556  29.1  4.5667   5 398    15.2 382.84
## 190  0.08370  45.0  3.44    0 0.4370 7.185  38.9  4.5667   5 398    15.2 396.90
## 191  0.09068  45.0  3.44    0 0.4370 6.951  21.5  6.4798   5 398    15.2 377.68
## 192  0.06911  45.0  3.44    0 0.4370 6.739  30.8  6.4798   5 398    15.2 389.71
## 193  0.08664  45.0  3.44    0 0.4370 7.178  26.3  6.4798   5 398    15.2 390.49
## 194  0.02187  60.0  2.93    0 0.4010 6.800   9.9  6.2196   1 265    15.6 393.37
## 195  0.01439  60.0  2.93    0 0.4010 6.604  18.8  6.2196   1 265    15.6 376.70
## 196  0.01381  80.0  0.46    0 0.4220 7.875  32.0  5.6484   4 255    14.4 394.23
## 197  0.04011  80.0  1.52    0 0.4040 7.287  34.1  7.3090   2 329    12.6 396.90
## 198  0.04666  80.0  1.52    0 0.4040 7.107  36.6  7.3090   2 329    12.6 354.31
## 199  0.03768  80.0  1.52    0 0.4040 7.274  38.3  7.3090   2 329    12.6 392.20
## 200  0.03150  95.0  1.47    0 0.4030 6.975  15.3  7.6534   3 402    17.0 396.90
## 201  0.01778  95.0  1.47    0 0.4030 7.135  13.9  7.6534   3 402    17.0 384.30
## 202  0.03445  82.5  2.03    0 0.4150 6.162  38.4  6.2700   2 348    14.7 393.77
## 203  0.02177  82.5  2.03    0 0.4150 7.610  15.7  6.2700   2 348    14.7 395.38
## 204  0.03510  95.0  2.68    0 0.4161 7.853  33.2  5.1180   4 224    14.7 392.78
## 205  0.02009  95.0  2.68    0 0.4161 8.034  31.9  5.1180   4 224    14.7 390.55
## 206  0.13642   0.0 10.59    0 0.4890 5.891  22.3  3.9454   4 277    18.6 396.90
## 207  0.22969   0.0 10.59    0 0.4890 6.326  52.5  4.3549   4 277    18.6 394.87
## 208  0.25199   0.0 10.59    0 0.4890 5.783  72.7  4.3549   4 277    18.6 389.43
## 209  0.13587   0.0 10.59    1 0.4890 6.064  59.1  4.2392   4 277    18.6 381.32
## 210  0.43571   0.0 10.59    1 0.4890 5.344 100.0  3.8750   4 277    18.6 396.90
## 211  0.17446   0.0 10.59    1 0.4890 5.960  92.1  3.8771   4 277    18.6 393.25
## 212  0.37578   0.0 10.59    1 0.4890 5.404  88.6  3.6650   4 277    18.6 395.24
## 213  0.21719   0.0 10.59    1 0.4890 5.807  53.8  3.6526   4 277    18.6 390.94
## 214  0.14052   0.0 10.59    0 0.4890 6.375  32.3  3.9454   4 277    18.6 385.81
## 215  0.28955   0.0 10.59    0 0.4890 5.412   9.8  3.5875   4 277    18.6 348.93
## 216  0.19802   0.0 10.59    0 0.4890 6.182  42.4  3.9454   4 277    18.6 393.63
## 217  0.04560   0.0 13.89    1 0.5500 5.888  56.0  3.1121   5 276    16.4 392.80
## 218  0.07013   0.0 13.89    0 0.5500 6.642  85.1  3.4211   5 276    16.4 392.78
## 219  0.11069   0.0 13.89    1 0.5500 5.951  93.8  2.8893   5 276    16.4 396.90
## 220  0.11425   0.0 13.89    1 0.5500 6.373  92.4  3.3633   5 276    16.4 393.74
## 221  0.35809   0.0  6.20    1 0.5070 6.951  88.5  2.8617   8 307    17.4 391.70
## 222  0.40771   0.0  6.20    1 0.5070 6.164  91.3  3.0480   8 307    17.4 395.24
## 223  0.62356   0.0  6.20    1 0.5070 6.879  77.7  3.2721   8 307    17.4 390.39
## 224  0.61470   0.0  6.20    0 0.5070 6.618  80.8  3.2721   8 307    17.4 396.90
## 225  0.31533   0.0  6.20    0 0.5040 8.266  78.3  2.8944   8 307    17.4 385.05
## 226  0.52693   0.0  6.20    0 0.5040 8.725  83.0  2.8944   8 307    17.4 382.00
## 227  0.38214   0.0  6.20    0 0.5040 8.040  86.5  3.2157   8 307    17.4 387.38
## 228  0.41238   0.0  6.20    0 0.5040 7.163  79.9  3.2157   8 307    17.4 372.08
## 229  0.29819   0.0  6.20    0 0.5040 7.686  17.0  3.3751   8 307    17.4 377.51
## 230  0.44178   0.0  6.20    0 0.5040 6.552  21.4  3.3751   8 307    17.4 380.34
## 231  0.53700   0.0  6.20    0 0.5040 5.981  68.1  3.6715   8 307    17.4 378.35
## 232  0.46296   0.0  6.20    0 0.5040 7.412  76.9  3.6715   8 307    17.4 376.14
## 233  0.57529   0.0  6.20    0 0.5070 8.337  73.3  3.8384   8 307    17.4 385.91
## 234  0.33147   0.0  6.20    0 0.5070 8.247  70.4  3.6519   8 307    17.4 378.95
## 235  0.44791   0.0  6.20    1 0.5070 6.726  66.5  3.6519   8 307    17.4 360.20
## 236  0.33045   0.0  6.20    0 0.5070 6.086  61.5  3.6519   8 307    17.4 376.75
## 237  0.52058   0.0  6.20    1 0.5070 6.631  76.5  4.1480   8 307    17.4 388.45
## 238  0.51183   0.0  6.20    0 0.5070 7.358  71.6  4.1480   8 307    17.4 390.07
## 239  0.08244  30.0  4.93    0 0.4280 6.481  18.5  6.1899   6 300    16.6 379.41
## 240  0.09252  30.0  4.93    0 0.4280 6.606  42.2  6.1899   6 300    16.6 383.78
## 241  0.11329  30.0  4.93    0 0.4280 6.897  54.3  6.3361   6 300    16.6 391.25
## 242  0.10612  30.0  4.93    0 0.4280 6.095  65.1  6.3361   6 300    16.6 394.62
## 243  0.10290  30.0  4.93    0 0.4280 6.358  52.9  7.0355   6 300    16.6 372.75
## 244  0.12757  30.0  4.93    0 0.4280 6.393   7.8  7.0355   6 300    16.6 374.71
## 245  0.20608  22.0  5.86    0 0.4310 5.593  76.5  7.9549   7 330    19.1 372.49
## 246  0.19133  22.0  5.86    0 0.4310 5.605  70.2  7.9549   7 330    19.1 389.13
## 247  0.33983  22.0  5.86    0 0.4310 6.108  34.9  8.0555   7 330    19.1 390.18
## 248  0.19657  22.0  5.86    0 0.4310 6.226  79.2  8.0555   7 330    19.1 376.14
## 249  0.16439  22.0  5.86    0 0.4310 6.433  49.1  7.8265   7 330    19.1 374.71
## 250  0.19073  22.0  5.86    0 0.4310 6.718  17.5  7.8265   7 330    19.1 393.74
## 251  0.14030  22.0  5.86    0 0.4310 6.487  13.0  7.3967   7 330    19.1 396.28
## 252  0.21409  22.0  5.86    0 0.4310 6.438   8.9  7.3967   7 330    19.1 377.07
## 253  0.08221  22.0  5.86    0 0.4310 6.957   6.8  8.9067   7 330    19.1 386.09
## 254  0.36894  22.0  5.86    0 0.4310 8.259   8.4  8.9067   7 330    19.1 396.90
## 255  0.04819  80.0  3.64    0 0.3920 6.108  32.0  9.2203   1 315    16.4 392.89
## 256  0.03548  80.0  3.64    0 0.3920 5.876  19.1  9.2203   1 315    16.4 395.18
## 257  0.01538  90.0  3.75    0 0.3940 7.454  34.2  6.3361   3 244    15.9 386.34
## 258  0.61154  20.0  3.97    0 0.6470 8.704  86.9  1.8010   5 264    13.0 389.70
## 259  0.66351  20.0  3.97    0 0.6470 7.333 100.0  1.8946   5 264    13.0 383.29
## 260  0.65665  20.0  3.97    0 0.6470 6.842 100.0  2.0107   5 264    13.0 391.93
## 261  0.54011  20.0  3.97    0 0.6470 7.203  81.8  2.1121   5 264    13.0 392.80
## 262  0.53412  20.0  3.97    0 0.6470 7.520  89.4  2.1398   5 264    13.0 388.37
## 263  0.52014  20.0  3.97    0 0.6470 8.398  91.5  2.2885   5 264    13.0 386.86
## 264  0.82526  20.0  3.97    0 0.6470 7.327  94.5  2.0788   5 264    13.0 393.42
## 265  0.55007  20.0  3.97    0 0.6470 7.206  91.6  1.9301   5 264    13.0 387.89
## 266  0.76162  20.0  3.97    0 0.6470 5.560  62.8  1.9865   5 264    13.0 392.40
## 267  0.78570  20.0  3.97    0 0.6470 7.014  84.6  2.1329   5 264    13.0 384.07
## 268  0.57834  20.0  3.97    0 0.5750 8.297  67.0  2.4216   5 264    13.0 384.54
## 269  0.54050  20.0  3.97    0 0.5750 7.470  52.6  2.8720   5 264    13.0 390.30
## 270  0.09065  20.0  6.96    1 0.4640 5.920  61.5  3.9175   3 223    18.6 391.34
## 271  0.29916  20.0  6.96    0 0.4640 5.856  42.1  4.4290   3 223    18.6 388.65
## 272  0.16211  20.0  6.96    0 0.4640 6.240  16.3  4.4290   3 223    18.6 396.90
## 273  0.11460  20.0  6.96    0 0.4640 6.538  58.7  3.9175   3 223    18.6 394.96
## 274  0.22188  20.0  6.96    1 0.4640 7.691  51.8  4.3665   3 223    18.6 390.77
## 275  0.05644  40.0  6.41    1 0.4470 6.758  32.9  4.0776   4 254    17.6 396.90
## 276  0.09604  40.0  6.41    0 0.4470 6.854  42.8  4.2673   4 254    17.6 396.90
## 277  0.10469  40.0  6.41    1 0.4470 7.267  49.0  4.7872   4 254    17.6 389.25
## 278  0.06127  40.0  6.41    1 0.4470 6.826  27.6  4.8628   4 254    17.6 393.45
## 279  0.07978  40.0  6.41    0 0.4470 6.482  32.1  4.1403   4 254    17.6 396.90
## 280  0.21038  20.0  3.33    0 0.4429 6.812  32.2  4.1007   5 216    14.9 396.90
## 281  0.03578  20.0  3.33    0 0.4429 7.820  64.5  4.6947   5 216    14.9 387.31
## 282  0.03705  20.0  3.33    0 0.4429 6.968  37.2  5.2447   5 216    14.9 392.23
## 283  0.06129  20.0  3.33    1 0.4429 7.645  49.7  5.2119   5 216    14.9 377.07
## 284  0.01501  90.0  1.21    1 0.4010 7.923  24.8  5.8850   1 198    13.6 395.52
## 285  0.00906  90.0  2.97    0 0.4000 7.088  20.8  7.3073   1 285    15.3 394.72
## 286  0.01096  55.0  2.25    0 0.3890 6.453  31.9  7.3073   1 300    15.3 394.72
## 287  0.01965  80.0  1.76    0 0.3850 6.230  31.5  9.0892   1 241    18.2 341.60
## 288  0.03871  52.5  5.32    0 0.4050 6.209  31.3  7.3172   6 293    16.6 396.90
## 289  0.04590  52.5  5.32    0 0.4050 6.315  45.6  7.3172   6 293    16.6 396.90
## 290  0.04297  52.5  5.32    0 0.4050 6.565  22.9  7.3172   6 293    16.6 371.72
## 291  0.03502  80.0  4.95    0 0.4110 6.861  27.9  5.1167   4 245    19.2 396.90
## 292  0.07886  80.0  4.95    0 0.4110 7.148  27.7  5.1167   4 245    19.2 396.90
## 293  0.03615  80.0  4.95    0 0.4110 6.630  23.4  5.1167   4 245    19.2 396.90
## 294  0.08265   0.0 13.92    0 0.4370 6.127  18.4  5.5027   4 289    16.0 396.90
## 295  0.08199   0.0 13.92    0 0.4370 6.009  42.3  5.5027   4 289    16.0 396.90
## 296  0.12932   0.0 13.92    0 0.4370 6.678  31.1  5.9604   4 289    16.0 396.90
## 297  0.05372   0.0 13.92    0 0.4370 6.549  51.0  5.9604   4 289    16.0 392.85
## 298  0.14103   0.0 13.92    0 0.4370 5.790  58.0  6.3200   4 289    16.0 396.90
## 299  0.06466  70.0  2.24    0 0.4000 6.345  20.1  7.8278   5 358    14.8 368.24
## 300  0.05561  70.0  2.24    0 0.4000 7.041  10.0  7.8278   5 358    14.8 371.58
## 301  0.04417  70.0  2.24    0 0.4000 6.871  47.4  7.8278   5 358    14.8 390.86
## 302  0.03537  34.0  6.09    0 0.4330 6.590  40.4  5.4917   7 329    16.1 395.75
## 303  0.09266  34.0  6.09    0 0.4330 6.495  18.4  5.4917   7 329    16.1 383.61
## 304  0.10000  34.0  6.09    0 0.4330 6.982  17.7  5.4917   7 329    16.1 390.43
## 305  0.05515  33.0  2.18    0 0.4720 7.236  41.1  4.0220   7 222    18.4 393.68
## 306  0.05479  33.0  2.18    0 0.4720 6.616  58.1  3.3700   7 222    18.4 393.36
## 307  0.07503  33.0  2.18    0 0.4720 7.420  71.9  3.0992   7 222    18.4 396.90
## 308  0.04932  33.0  2.18    0 0.4720 6.849  70.3  3.1827   7 222    18.4 396.90
## 309  0.49298   0.0  9.90    0 0.5440 6.635  82.5  3.3175   4 304    18.4 396.90
## 310  0.34940   0.0  9.90    0 0.5440 5.972  76.7  3.1025   4 304    18.4 396.24
## 311  2.63548   0.0  9.90    0 0.5440 4.973  37.8  2.5194   4 304    18.4 350.45
## 312  0.79041   0.0  9.90    0 0.5440 6.122  52.8  2.6403   4 304    18.4 396.90
## 313  0.26169   0.0  9.90    0 0.5440 6.023  90.4  2.8340   4 304    18.4 396.30
## 314  0.26938   0.0  9.90    0 0.5440 6.266  82.8  3.2628   4 304    18.4 393.39
## 315  0.36920   0.0  9.90    0 0.5440 6.567  87.3  3.6023   4 304    18.4 395.69
## 316  0.25356   0.0  9.90    0 0.5440 5.705  77.7  3.9450   4 304    18.4 396.42
## 317  0.31827   0.0  9.90    0 0.5440 5.914  83.2  3.9986   4 304    18.4 390.70
## 318  0.24522   0.0  9.90    0 0.5440 5.782  71.7  4.0317   4 304    18.4 396.90
## 319  0.40202   0.0  9.90    0 0.5440 6.382  67.2  3.5325   4 304    18.4 395.21
## 320  0.47547   0.0  9.90    0 0.5440 6.113  58.8  4.0019   4 304    18.4 396.23
## 321  0.16760   0.0  7.38    0 0.4930 6.426  52.3  4.5404   5 287    19.6 396.90
## 322  0.18159   0.0  7.38    0 0.4930 6.376  54.3  4.5404   5 287    19.6 396.90
## 323  0.35114   0.0  7.38    0 0.4930 6.041  49.9  4.7211   5 287    19.6 396.90
## 324  0.28392   0.0  7.38    0 0.4930 5.708  74.3  4.7211   5 287    19.6 391.13
## 325  0.34109   0.0  7.38    0 0.4930 6.415  40.1  4.7211   5 287    19.6 396.90
## 326  0.19186   0.0  7.38    0 0.4930 6.431  14.7  5.4159   5 287    19.6 393.68
## 327  0.30347   0.0  7.38    0 0.4930 6.312  28.9  5.4159   5 287    19.6 396.90
## 328  0.24103   0.0  7.38    0 0.4930 6.083  43.7  5.4159   5 287    19.6 396.90
## 329  0.06617   0.0  3.24    0 0.4600 5.868  25.8  5.2146   4 430    16.9 382.44
## 330  0.06724   0.0  3.24    0 0.4600 6.333  17.2  5.2146   4 430    16.9 375.21
## 331  0.04544   0.0  3.24    0 0.4600 6.144  32.2  5.8736   4 430    16.9 368.57
## 332  0.05023  35.0  6.06    0 0.4379 5.706  28.4  6.6407   1 304    16.9 394.02
## 333  0.03466  35.0  6.06    0 0.4379 6.031  23.3  6.6407   1 304    16.9 362.25
## 334  0.05083   0.0  5.19    0 0.5150 6.316  38.1  6.4584   5 224    20.2 389.71
## 335  0.03738   0.0  5.19    0 0.5150 6.310  38.5  6.4584   5 224    20.2 389.40
## 336  0.03961   0.0  5.19    0 0.5150 6.037  34.5  5.9853   5 224    20.2 396.90
## 337  0.03427   0.0  5.19    0 0.5150 5.869  46.3  5.2311   5 224    20.2 396.90
## 338  0.03041   0.0  5.19    0 0.5150 5.895  59.6  5.6150   5 224    20.2 394.81
## 339  0.03306   0.0  5.19    0 0.5150 6.059  37.3  4.8122   5 224    20.2 396.14
## 340  0.05497   0.0  5.19    0 0.5150 5.985  45.4  4.8122   5 224    20.2 396.90
## 341  0.06151   0.0  5.19    0 0.5150 5.968  58.5  4.8122   5 224    20.2 396.90
## 342  0.01301  35.0  1.52    0 0.4420 7.241  49.3  7.0379   1 284    15.5 394.74
## 343  0.02498   0.0  1.89    0 0.5180 6.540  59.7  6.2669   1 422    15.9 389.96
## 344  0.02543  55.0  3.78    0 0.4840 6.696  56.4  5.7321   5 370    17.6 396.90
## 345  0.03049  55.0  3.78    0 0.4840 6.874  28.1  6.4654   5 370    17.6 387.97
## 346  0.03113   0.0  4.39    0 0.4420 6.014  48.5  8.0136   3 352    18.8 385.64
## 347  0.06162   0.0  4.39    0 0.4420 5.898  52.3  8.0136   3 352    18.8 364.61
## 348  0.01870  85.0  4.15    0 0.4290 6.516  27.7  8.5353   4 351    17.9 392.43
## 349  0.01501  80.0  2.01    0 0.4350 6.635  29.7  8.3440   4 280    17.0 390.94
## 350  0.02899  40.0  1.25    0 0.4290 6.939  34.5  8.7921   1 335    19.7 389.85
## 351  0.06211  40.0  1.25    0 0.4290 6.490  44.4  8.7921   1 335    19.7 396.90
## 352  0.07950  60.0  1.69    0 0.4110 6.579  35.9 10.7103   4 411    18.3 370.78
## 353  0.07244  60.0  1.69    0 0.4110 5.884  18.5 10.7103   4 411    18.3 392.33
## 354  0.01709  90.0  2.02    0 0.4100 6.728  36.1 12.1265   5 187    17.0 384.46
## 355  0.04301  80.0  1.91    0 0.4130 5.663  21.9 10.5857   4 334    22.0 382.80
## 356  0.10659  80.0  1.91    0 0.4130 5.936  19.5 10.5857   4 334    22.0 376.04
## 357  8.98296   0.0 18.10    1 0.7700 6.212  97.4  2.1222  24 666    20.2 377.73
## 358  3.84970   0.0 18.10    1 0.7700 6.395  91.0  2.5052  24 666    20.2 391.34
## 359  5.20177   0.0 18.10    1 0.7700 6.127  83.4  2.7227  24 666    20.2 395.43
## 360  4.26131   0.0 18.10    0 0.7700 6.112  81.3  2.5091  24 666    20.2 390.74
## 361  4.54192   0.0 18.10    0 0.7700 6.398  88.0  2.5182  24 666    20.2 374.56
## 362  3.83684   0.0 18.10    0 0.7700 6.251  91.1  2.2955  24 666    20.2 350.65
## 363  3.67822   0.0 18.10    0 0.7700 5.362  96.2  2.1036  24 666    20.2 380.79
## 364  4.22239   0.0 18.10    1 0.7700 5.803  89.0  1.9047  24 666    20.2 353.04
## 365  3.47428   0.0 18.10    1 0.7180 8.780  82.9  1.9047  24 666    20.2 354.55
## 366  4.55587   0.0 18.10    0 0.7180 3.561  87.9  1.6132  24 666    20.2 354.70
## 367  3.69695   0.0 18.10    0 0.7180 4.963  91.4  1.7523  24 666    20.2 316.03
## 368 13.52220   0.0 18.10    0 0.6310 3.863 100.0  1.5106  24 666    20.2 131.42
## 369  4.89822   0.0 18.10    0 0.6310 4.970 100.0  1.3325  24 666    20.2 375.52
## 370  5.66998   0.0 18.10    1 0.6310 6.683  96.8  1.3567  24 666    20.2 375.33
## 371  6.53876   0.0 18.10    1 0.6310 7.016  97.5  1.2024  24 666    20.2 392.05
## 372  9.23230   0.0 18.10    0 0.6310 6.216 100.0  1.1691  24 666    20.2 366.15
## 373  8.26725   0.0 18.10    1 0.6680 5.875  89.6  1.1296  24 666    20.2 347.88
## 374 11.10810   0.0 18.10    0 0.6680 4.906 100.0  1.1742  24 666    20.2 396.90
## 375 18.49820   0.0 18.10    0 0.6680 4.138 100.0  1.1370  24 666    20.2 396.90
## 376 19.60910   0.0 18.10    0 0.6710 7.313  97.9  1.3163  24 666    20.2 396.90
## 377 15.28800   0.0 18.10    0 0.6710 6.649  93.3  1.3449  24 666    20.2 363.02
## 378  9.82349   0.0 18.10    0 0.6710 6.794  98.8  1.3580  24 666    20.2 396.90
## 379 23.64820   0.0 18.10    0 0.6710 6.380  96.2  1.3861  24 666    20.2 396.90
## 380 17.86670   0.0 18.10    0 0.6710 6.223 100.0  1.3861  24 666    20.2 393.74
## 381 88.97620   0.0 18.10    0 0.6710 6.968  91.9  1.4165  24 666    20.2 396.90
## 382 15.87440   0.0 18.10    0 0.6710 6.545  99.1  1.5192  24 666    20.2 396.90
## 383  9.18702   0.0 18.10    0 0.7000 5.536 100.0  1.5804  24 666    20.2 396.90
## 384  7.99248   0.0 18.10    0 0.7000 5.520 100.0  1.5331  24 666    20.2 396.90
## 385 20.08490   0.0 18.10    0 0.7000 4.368  91.2  1.4395  24 666    20.2 285.83
## 386 16.81180   0.0 18.10    0 0.7000 5.277  98.1  1.4261  24 666    20.2 396.90
## 387 24.39380   0.0 18.10    0 0.7000 4.652 100.0  1.4672  24 666    20.2 396.90
## 388 22.59710   0.0 18.10    0 0.7000 5.000  89.5  1.5184  24 666    20.2 396.90
## 389 14.33370   0.0 18.10    0 0.7000 4.880 100.0  1.5895  24 666    20.2 372.92
## 390  8.15174   0.0 18.10    0 0.7000 5.390  98.9  1.7281  24 666    20.2 396.90
## 391  6.96215   0.0 18.10    0 0.7000 5.713  97.0  1.9265  24 666    20.2 394.43
## 392  5.29305   0.0 18.10    0 0.7000 6.051  82.5  2.1678  24 666    20.2 378.38
## 393 11.57790   0.0 18.10    0 0.7000 5.036  97.0  1.7700  24 666    20.2 396.90
## 394  8.64476   0.0 18.10    0 0.6930 6.193  92.6  1.7912  24 666    20.2 396.90
## 395 13.35980   0.0 18.10    0 0.6930 5.887  94.7  1.7821  24 666    20.2 396.90
## 396  8.71675   0.0 18.10    0 0.6930 6.471  98.8  1.7257  24 666    20.2 391.98
## 397  5.87205   0.0 18.10    0 0.6930 6.405  96.0  1.6768  24 666    20.2 396.90
## 398  7.67202   0.0 18.10    0 0.6930 5.747  98.9  1.6334  24 666    20.2 393.10
## 399 38.35180   0.0 18.10    0 0.6930 5.453 100.0  1.4896  24 666    20.2 396.90
## 400  9.91655   0.0 18.10    0 0.6930 5.852  77.8  1.5004  24 666    20.2 338.16
## 401 25.04610   0.0 18.10    0 0.6930 5.987 100.0  1.5888  24 666    20.2 396.90
## 402 14.23620   0.0 18.10    0 0.6930 6.343 100.0  1.5741  24 666    20.2 396.90
## 403  9.59571   0.0 18.10    0 0.6930 6.404 100.0  1.6390  24 666    20.2 376.11
## 404 24.80170   0.0 18.10    0 0.6930 5.349  96.0  1.7028  24 666    20.2 396.90
## 405 41.52920   0.0 18.10    0 0.6930 5.531  85.4  1.6074  24 666    20.2 329.46
## 406 67.92080   0.0 18.10    0 0.6930 5.683 100.0  1.4254  24 666    20.2 384.97
## 407 20.71620   0.0 18.10    0 0.6590 4.138 100.0  1.1781  24 666    20.2 370.22
## 408 11.95110   0.0 18.10    0 0.6590 5.608 100.0  1.2852  24 666    20.2 332.09
## 409  7.40389   0.0 18.10    0 0.5970 5.617  97.9  1.4547  24 666    20.2 314.64
## 410 14.43830   0.0 18.10    0 0.5970 6.852 100.0  1.4655  24 666    20.2 179.36
## 411 51.13580   0.0 18.10    0 0.5970 5.757 100.0  1.4130  24 666    20.2   2.60
## 412 14.05070   0.0 18.10    0 0.5970 6.657 100.0  1.5275  24 666    20.2  35.05
## 413 18.81100   0.0 18.10    0 0.5970 4.628 100.0  1.5539  24 666    20.2  28.79
## 414 28.65580   0.0 18.10    0 0.5970 5.155 100.0  1.5894  24 666    20.2 210.97
## 415 45.74610   0.0 18.10    0 0.6930 4.519 100.0  1.6582  24 666    20.2  88.27
## 416 18.08460   0.0 18.10    0 0.6790 6.434 100.0  1.8347  24 666    20.2  27.25
## 417 10.83420   0.0 18.10    0 0.6790 6.782  90.8  1.8195  24 666    20.2  21.57
## 418 25.94060   0.0 18.10    0 0.6790 5.304  89.1  1.6475  24 666    20.2 127.36
## 419 73.53410   0.0 18.10    0 0.6790 5.957 100.0  1.8026  24 666    20.2  16.45
## 420 11.81230   0.0 18.10    0 0.7180 6.824  76.5  1.7940  24 666    20.2  48.45
## 421 11.08740   0.0 18.10    0 0.7180 6.411 100.0  1.8589  24 666    20.2 318.75
## 422  7.02259   0.0 18.10    0 0.7180 6.006  95.3  1.8746  24 666    20.2 319.98
## 423 12.04820   0.0 18.10    0 0.6140 5.648  87.6  1.9512  24 666    20.2 291.55
## 424  7.05042   0.0 18.10    0 0.6140 6.103  85.1  2.0218  24 666    20.2   2.52
## 425  8.79212   0.0 18.10    0 0.5840 5.565  70.6  2.0635  24 666    20.2   3.65
## 426 15.86030   0.0 18.10    0 0.6790 5.896  95.4  1.9096  24 666    20.2   7.68
## 427 12.24720   0.0 18.10    0 0.5840 5.837  59.7  1.9976  24 666    20.2  24.65
## 428 37.66190   0.0 18.10    0 0.6790 6.202  78.7  1.8629  24 666    20.2  18.82
## 429  7.36711   0.0 18.10    0 0.6790 6.193  78.1  1.9356  24 666    20.2  96.73
## 430  9.33889   0.0 18.10    0 0.6790 6.380  95.6  1.9682  24 666    20.2  60.72
## 431  8.49213   0.0 18.10    0 0.5840 6.348  86.1  2.0527  24 666    20.2  83.45
## 432 10.06230   0.0 18.10    0 0.5840 6.833  94.3  2.0882  24 666    20.2  81.33
## 433  6.44405   0.0 18.10    0 0.5840 6.425  74.8  2.2004  24 666    20.2  97.95
## 434  5.58107   0.0 18.10    0 0.7130 6.436  87.9  2.3158  24 666    20.2 100.19
## 435 13.91340   0.0 18.10    0 0.7130 6.208  95.0  2.2222  24 666    20.2 100.63
## 436 11.16040   0.0 18.10    0 0.7400 6.629  94.6  2.1247  24 666    20.2 109.85
## 437 14.42080   0.0 18.10    0 0.7400 6.461  93.3  2.0026  24 666    20.2  27.49
## 438 15.17720   0.0 18.10    0 0.7400 6.152 100.0  1.9142  24 666    20.2   9.32
## 439 13.67810   0.0 18.10    0 0.7400 5.935  87.9  1.8206  24 666    20.2  68.95
## 440  9.39063   0.0 18.10    0 0.7400 5.627  93.9  1.8172  24 666    20.2 396.90
## 441 22.05110   0.0 18.10    0 0.7400 5.818  92.4  1.8662  24 666    20.2 391.45
## 442  9.72418   0.0 18.10    0 0.7400 6.406  97.2  2.0651  24 666    20.2 385.96
## 443  5.66637   0.0 18.10    0 0.7400 6.219 100.0  2.0048  24 666    20.2 395.69
## 444  9.96654   0.0 18.10    0 0.7400 6.485 100.0  1.9784  24 666    20.2 386.73
## 445 12.80230   0.0 18.10    0 0.7400 5.854  96.6  1.8956  24 666    20.2 240.52
## 446 10.67180   0.0 18.10    0 0.7400 6.459  94.8  1.9879  24 666    20.2  43.06
## 447  6.28807   0.0 18.10    0 0.7400 6.341  96.4  2.0720  24 666    20.2 318.01
## 448  9.92485   0.0 18.10    0 0.7400 6.251  96.6  2.1980  24 666    20.2 388.52
## 449  9.32909   0.0 18.10    0 0.7130 6.185  98.7  2.2616  24 666    20.2 396.90
## 450  7.52601   0.0 18.10    0 0.7130 6.417  98.3  2.1850  24 666    20.2 304.21
## 451  6.71772   0.0 18.10    0 0.7130 6.749  92.6  2.3236  24 666    20.2   0.32
## 452  5.44114   0.0 18.10    0 0.7130 6.655  98.2  2.3552  24 666    20.2 355.29
## 453  5.09017   0.0 18.10    0 0.7130 6.297  91.8  2.3682  24 666    20.2 385.09
## 454  8.24809   0.0 18.10    0 0.7130 7.393  99.3  2.4527  24 666    20.2 375.87
## 455  9.51363   0.0 18.10    0 0.7130 6.728  94.1  2.4961  24 666    20.2   6.68
## 456  4.75237   0.0 18.10    0 0.7130 6.525  86.5  2.4358  24 666    20.2  50.92
## 457  4.66883   0.0 18.10    0 0.7130 5.976  87.9  2.5806  24 666    20.2  10.48
## 458  8.20058   0.0 18.10    0 0.7130 5.936  80.3  2.7792  24 666    20.2   3.50
## 459  7.75223   0.0 18.10    0 0.7130 6.301  83.7  2.7831  24 666    20.2 272.21
## 460  6.80117   0.0 18.10    0 0.7130 6.081  84.4  2.7175  24 666    20.2 396.90
## 461  4.81213   0.0 18.10    0 0.7130 6.701  90.0  2.5975  24 666    20.2 255.23
## 462  3.69311   0.0 18.10    0 0.7130 6.376  88.4  2.5671  24 666    20.2 391.43
## 463  6.65492   0.0 18.10    0 0.7130 6.317  83.0  2.7344  24 666    20.2 396.90
## 464  5.82115   0.0 18.10    0 0.7130 6.513  89.9  2.8016  24 666    20.2 393.82
## 465  7.83932   0.0 18.10    0 0.6550 6.209  65.4  2.9634  24 666    20.2 396.90
## 466  3.16360   0.0 18.10    0 0.6550 5.759  48.2  3.0665  24 666    20.2 334.40
## 467  3.77498   0.0 18.10    0 0.6550 5.952  84.7  2.8715  24 666    20.2  22.01
## 468  4.42228   0.0 18.10    0 0.5840 6.003  94.5  2.5403  24 666    20.2 331.29
## 469 15.57570   0.0 18.10    0 0.5800 5.926  71.0  2.9084  24 666    20.2 368.74
## 470 13.07510   0.0 18.10    0 0.5800 5.713  56.7  2.8237  24 666    20.2 396.90
## 471  4.34879   0.0 18.10    0 0.5800 6.167  84.0  3.0334  24 666    20.2 396.90
## 472  4.03841   0.0 18.10    0 0.5320 6.229  90.7  3.0993  24 666    20.2 395.33
## 473  3.56868   0.0 18.10    0 0.5800 6.437  75.0  2.8965  24 666    20.2 393.37
## 474  4.64689   0.0 18.10    0 0.6140 6.980  67.6  2.5329  24 666    20.2 374.68
## 475  8.05579   0.0 18.10    0 0.5840 5.427  95.4  2.4298  24 666    20.2 352.58
## 476  6.39312   0.0 18.10    0 0.5840 6.162  97.4  2.2060  24 666    20.2 302.76
## 477  4.87141   0.0 18.10    0 0.6140 6.484  93.6  2.3053  24 666    20.2 396.21
## 478 15.02340   0.0 18.10    0 0.6140 5.304  97.3  2.1007  24 666    20.2 349.48
## 479 10.23300   0.0 18.10    0 0.6140 6.185  96.7  2.1705  24 666    20.2 379.70
## 480 14.33370   0.0 18.10    0 0.6140 6.229  88.0  1.9512  24 666    20.2 383.32
## 481  5.82401   0.0 18.10    0 0.5320 6.242  64.7  3.4242  24 666    20.2 396.90
## 482  5.70818   0.0 18.10    0 0.5320 6.750  74.9  3.3317  24 666    20.2 393.07
## 483  5.73116   0.0 18.10    0 0.5320 7.061  77.0  3.4106  24 666    20.2 395.28
## 484  2.81838   0.0 18.10    0 0.5320 5.762  40.3  4.0983  24 666    20.2 392.92
## 485  2.37857   0.0 18.10    0 0.5830 5.871  41.9  3.7240  24 666    20.2 370.73
## 486  3.67367   0.0 18.10    0 0.5830 6.312  51.9  3.9917  24 666    20.2 388.62
## 487  5.69175   0.0 18.10    0 0.5830 6.114  79.8  3.5459  24 666    20.2 392.68
## 488  4.83567   0.0 18.10    0 0.5830 5.905  53.2  3.1523  24 666    20.2 388.22
## 489  0.15086   0.0 27.74    0 0.6090 5.454  92.7  1.8209   4 711    20.1 395.09
## 490  0.18337   0.0 27.74    0 0.6090 5.414  98.3  1.7554   4 711    20.1 344.05
## 491  0.20746   0.0 27.74    0 0.6090 5.093  98.0  1.8226   4 711    20.1 318.43
## 492  0.10574   0.0 27.74    0 0.6090 5.983  98.8  1.8681   4 711    20.1 390.11
## 493  0.11132   0.0 27.74    0 0.6090 5.983  83.5  2.1099   4 711    20.1 396.90
## 494  0.17331   0.0  9.69    0 0.5850 5.707  54.0  2.3817   6 391    19.2 396.90
## 495  0.27957   0.0  9.69    0 0.5850 5.926  42.6  2.3817   6 391    19.2 396.90
## 496  0.17899   0.0  9.69    0 0.5850 5.670  28.8  2.7986   6 391    19.2 393.29
## 497  0.28960   0.0  9.69    0 0.5850 5.390  72.9  2.7986   6 391    19.2 396.90
## 498  0.26838   0.0  9.69    0 0.5850 5.794  70.6  2.8927   6 391    19.2 396.90
## 499  0.23912   0.0  9.69    0 0.5850 6.019  65.3  2.4091   6 391    19.2 396.90
## 500  0.17783   0.0  9.69    0 0.5850 5.569  73.5  2.3999   6 391    19.2 395.77
## 501  0.22438   0.0  9.69    0 0.5850 6.027  79.7  2.4982   6 391    19.2 396.90
## 502  0.06263   0.0 11.93    0 0.5730 6.593  69.1  2.4786   1 273    21.0 391.99
## 503  0.04527   0.0 11.93    0 0.5730 6.120  76.7  2.2875   1 273    21.0 396.90
## 504  0.06076   0.0 11.93    0 0.5730 6.976  91.0  2.1675   1 273    21.0 396.90
## 505  0.10959   0.0 11.93    0 0.5730 6.794  89.3  2.3889   1 273    21.0 393.45
## 506  0.04741   0.0 11.93    0 0.5730 6.030  80.8  2.5050   1 273    21.0 396.90
##     lstat medv
## 1    4.98 24.0
## 2    9.14 21.6
## 3    4.03 34.7
## 4    2.94 33.4
## 5    5.33 36.2
## 6    5.21 28.7
## 7   12.43 22.9
## 8   19.15 27.1
## 9   29.93 16.5
## 10  17.10 18.9
## 11  20.45 15.0
## 12  13.27 18.9
## 13  15.71 21.7
## 14   8.26 20.4
## 15  10.26 18.2
## 16   8.47 19.9
## 17   6.58 23.1
## 18  14.67 17.5
## 19  11.69 20.2
## 20  11.28 18.2
## 21  21.02 13.6
## 22  13.83 19.6
## 23  18.72 15.2
## 24  19.88 14.5
## 25  16.30 15.6
## 26  16.51 13.9
## 27  14.81 16.6
## 28  17.28 14.8
## 29  12.80 18.4
## 30  11.98 21.0
## 31  22.60 12.7
## 32  13.04 14.5
## 33  27.71 13.2
## 34  18.35 13.1
## 35  20.34 13.5
## 36   9.68 18.9
## 37  11.41 20.0
## 38   8.77 21.0
## 39  10.13 24.7
## 40   4.32 30.8
## 41   1.98 34.9
## 42   4.84 26.6
## 43   5.81 25.3
## 44   7.44 24.7
## 45   9.55 21.2
## 46  10.21 19.3
## 47  14.15 20.0
## 48  18.80 16.6
## 49  30.81 14.4
## 50  16.20 19.4
## 51  13.45 19.7
## 52   9.43 20.5
## 53   5.28 25.0
## 54   8.43 23.4
## 55  14.80 18.9
## 56   4.81 35.4
## 57   5.77 24.7
## 58   3.95 31.6
## 59   6.86 23.3
## 60   9.22 19.6
## 61  13.15 18.7
## 62  14.44 16.0
## 63   6.73 22.2
## 64   9.50 25.0
## 65   8.05 33.0
## 66   4.67 23.5
## 67  10.24 19.4
## 68   8.10 22.0
## 69  13.09 17.4
## 70   8.79 20.9
## 71   6.72 24.2
## 72   9.88 21.7
## 73   5.52 22.8
## 74   7.54 23.4
## 75   6.78 24.1
## 76   8.94 21.4
## 77  11.97 20.0
## 78  10.27 20.8
## 79  12.34 21.2
## 80   9.10 20.3
## 81   5.29 28.0
## 82   7.22 23.9
## 83   6.72 24.8
## 84   7.51 22.9
## 85   9.62 23.9
## 86   6.53 26.6
## 87  12.86 22.5
## 88   8.44 22.2
## 89   5.50 23.6
## 90   5.70 28.7
## 91   8.81 22.6
## 92   8.20 22.0
## 93   8.16 22.9
## 94   6.21 25.0
## 95  10.59 20.6
## 96   6.65 28.4
## 97  11.34 21.4
## 98   4.21 38.7
## 99   3.57 43.8
## 100  6.19 33.2
## 101  9.42 27.5
## 102  7.67 26.5
## 103 10.63 18.6
## 104 13.44 19.3
## 105 12.33 20.1
## 106 16.47 19.5
## 107 18.66 19.5
## 108 14.09 20.4
## 109 12.27 19.8
## 110 15.55 19.4
## 111 13.00 21.7
## 112 10.16 22.8
## 113 16.21 18.8
## 114 17.09 18.7
## 115 10.45 18.5
## 116 15.76 18.3
## 117 12.04 21.2
## 118 10.30 19.2
## 119 15.37 20.4
## 120 13.61 19.3
## 121 14.37 22.0
## 122 14.27 20.3
## 123 17.93 20.5
## 124 25.41 17.3
## 125 17.58 18.8
## 126 14.81 21.4
## 127 27.26 15.7
## 128 17.19 16.2
## 129 15.39 18.0
## 130 18.34 14.3
## 131 12.60 19.2
## 132 12.26 19.6
## 133 11.12 23.0
## 134 15.03 18.4
## 135 17.31 15.6
## 136 16.96 18.1
## 137 16.90 17.4
## 138 14.59 17.1
## 139 21.32 13.3
## 140 18.46 17.8
## 141 24.16 14.0
## 142 34.41 14.4
## 143 26.82 13.4
## 144 26.42 15.6
## 145 29.29 11.8
## 146 27.80 13.8
## 147 16.65 15.6
## 148 29.53 14.6
## 149 28.32 17.8
## 150 21.45 15.4
## 151 14.10 21.5
## 152 13.28 19.6
## 153 12.12 15.3
## 154 15.79 19.4
## 155 15.12 17.0
## 156 15.02 15.6
## 157 16.14 13.1
## 158  4.59 41.3
## 159  6.43 24.3
## 160  7.39 23.3
## 161  5.50 27.0
## 162  1.73 50.0
## 163  1.92 50.0
## 164  3.32 50.0
## 165 11.64 22.7
## 166  9.81 25.0
## 167  3.70 50.0
## 168 12.14 23.8
## 169 11.10 23.8
## 170 11.32 22.3
## 171 14.43 17.4
## 172 12.03 19.1
## 173 14.69 23.1
## 174  9.04 23.6
## 175  9.64 22.6
## 176  5.33 29.4
## 177 10.11 23.2
## 178  6.29 24.6
## 179  6.92 29.9
## 180  5.04 37.2
## 181  7.56 39.8
## 182  9.45 36.2
## 183  4.82 37.9
## 184  5.68 32.5
## 185 13.98 26.4
## 186 13.15 29.6
## 187  4.45 50.0
## 188  6.68 32.0
## 189  4.56 29.8
## 190  5.39 34.9
## 191  5.10 37.0
## 192  4.69 30.5
## 193  2.87 36.4
## 194  5.03 31.1
## 195  4.38 29.1
## 196  2.97 50.0
## 197  4.08 33.3
## 198  8.61 30.3
## 199  6.62 34.6
## 200  4.56 34.9
## 201  4.45 32.9
## 202  7.43 24.1
## 203  3.11 42.3
## 204  3.81 48.5
## 205  2.88 50.0
## 206 10.87 22.6
## 207 10.97 24.4
## 208 18.06 22.5
## 209 14.66 24.4
## 210 23.09 20.0
## 211 17.27 21.7
## 212 23.98 19.3
## 213 16.03 22.4
## 214  9.38 28.1
## 215 29.55 23.7
## 216  9.47 25.0
## 217 13.51 23.3
## 218  9.69 28.7
## 219 17.92 21.5
## 220 10.50 23.0
## 221  9.71 26.7
## 222 21.46 21.7
## 223  9.93 27.5
## 224  7.60 30.1
## 225  4.14 44.8
## 226  4.63 50.0
## 227  3.13 37.6
## 228  6.36 31.6
## 229  3.92 46.7
## 230  3.76 31.5
## 231 11.65 24.3
## 232  5.25 31.7
## 233  2.47 41.7
## 234  3.95 48.3
## 235  8.05 29.0
## 236 10.88 24.0
## 237  9.54 25.1
## 238  4.73 31.5
## 239  6.36 23.7
## 240  7.37 23.3
## 241 11.38 22.0
## 242 12.40 20.1
## 243 11.22 22.2
## 244  5.19 23.7
## 245 12.50 17.6
## 246 18.46 18.5
## 247  9.16 24.3
## 248 10.15 20.5
## 249  9.52 24.5
## 250  6.56 26.2
## 251  5.90 24.4
## 252  3.59 24.8
## 253  3.53 29.6
## 254  3.54 42.8
## 255  6.57 21.9
## 256  9.25 20.9
## 257  3.11 44.0
## 258  5.12 50.0
## 259  7.79 36.0
## 260  6.90 30.1
## 261  9.59 33.8
## 262  7.26 43.1
## 263  5.91 48.8
## 264 11.25 31.0
## 265  8.10 36.5
## 266 10.45 22.8
## 267 14.79 30.7
## 268  7.44 50.0
## 269  3.16 43.5
## 270 13.65 20.7
## 271 13.00 21.1
## 272  6.59 25.2
## 273  7.73 24.4
## 274  6.58 35.2
## 275  3.53 32.4
## 276  2.98 32.0
## 277  6.05 33.2
## 278  4.16 33.1
## 279  7.19 29.1
## 280  4.85 35.1
## 281  3.76 45.4
## 282  4.59 35.4
## 283  3.01 46.0
## 284  3.16 50.0
## 285  7.85 32.2
## 286  8.23 22.0
## 287 12.93 20.1
## 288  7.14 23.2
## 289  7.60 22.3
## 290  9.51 24.8
## 291  3.33 28.5
## 292  3.56 37.3
## 293  4.70 27.9
## 294  8.58 23.9
## 295 10.40 21.7
## 296  6.27 28.6
## 297  7.39 27.1
## 298 15.84 20.3
## 299  4.97 22.5
## 300  4.74 29.0
## 301  6.07 24.8
## 302  9.50 22.0
## 303  8.67 26.4
## 304  4.86 33.1
## 305  6.93 36.1
## 306  8.93 28.4
## 307  6.47 33.4
## 308  7.53 28.2
## 309  4.54 22.8
## 310  9.97 20.3
## 311 12.64 16.1
## 312  5.98 22.1
## 313 11.72 19.4
## 314  7.90 21.6
## 315  9.28 23.8
## 316 11.50 16.2
## 317 18.33 17.8
## 318 15.94 19.8
## 319 10.36 23.1
## 320 12.73 21.0
## 321  7.20 23.8
## 322  6.87 23.1
## 323  7.70 20.4
## 324 11.74 18.5
## 325  6.12 25.0
## 326  5.08 24.6
## 327  6.15 23.0
## 328 12.79 22.2
## 329  9.97 19.3
## 330  7.34 22.6
## 331  9.09 19.8
## 332 12.43 17.1
## 333  7.83 19.4
## 334  5.68 22.2
## 335  6.75 20.7
## 336  8.01 21.1
## 337  9.80 19.5
## 338 10.56 18.5
## 339  8.51 20.6
## 340  9.74 19.0
## 341  9.29 18.7
## 342  5.49 32.7
## 343  8.65 16.5
## 344  7.18 23.9
## 345  4.61 31.2
## 346 10.53 17.5
## 347 12.67 17.2
## 348  6.36 23.1
## 349  5.99 24.5
## 350  5.89 26.6
## 351  5.98 22.9
## 352  5.49 24.1
## 353  7.79 18.6
## 354  4.50 30.1
## 355  8.05 18.2
## 356  5.57 20.6
## 357 17.60 17.8
## 358 13.27 21.7
## 359 11.48 22.7
## 360 12.67 22.6
## 361  7.79 25.0
## 362 14.19 19.9
## 363 10.19 20.8
## 364 14.64 16.8
## 365  5.29 21.9
## 366  7.12 27.5
## 367 14.00 21.9
## 368 13.33 23.1
## 369  3.26 50.0
## 370  3.73 50.0
## 371  2.96 50.0
## 372  9.53 50.0
## 373  8.88 50.0
## 374 34.77 13.8
## 375 37.97 13.8
## 376 13.44 15.0
## 377 23.24 13.9
## 378 21.24 13.3
## 379 23.69 13.1
## 380 21.78 10.2
## 381 17.21 10.4
## 382 21.08 10.9
## 383 23.60 11.3
## 384 24.56 12.3
## 385 30.63  8.8
## 386 30.81  7.2
## 387 28.28 10.5
## 388 31.99  7.4
## 389 30.62 10.2
## 390 20.85 11.5
## 391 17.11 15.1
## 392 18.76 23.2
## 393 25.68  9.7
## 394 15.17 13.8
## 395 16.35 12.7
## 396 17.12 13.1
## 397 19.37 12.5
## 398 19.92  8.5
## 399 30.59  5.0
## 400 29.97  6.3
## 401 26.77  5.6
## 402 20.32  7.2
## 403 20.31 12.1
## 404 19.77  8.3
## 405 27.38  8.5
## 406 22.98  5.0
## 407 23.34 11.9
## 408 12.13 27.9
## 409 26.40 17.2
## 410 19.78 27.5
## 411 10.11 15.0
## 412 21.22 17.2
## 413 34.37 17.9
## 414 20.08 16.3
## 415 36.98  7.0
## 416 29.05  7.2
## 417 25.79  7.5
## 418 26.64 10.4
## 419 20.62  8.8
## 420 22.74  8.4
## 421 15.02 16.7
## 422 15.70 14.2
## 423 14.10 20.8
## 424 23.29 13.4
## 425 17.16 11.7
## 426 24.39  8.3
## 427 15.69 10.2
## 428 14.52 10.9
## 429 21.52 11.0
## 430 24.08  9.5
## 431 17.64 14.5
## 432 19.69 14.1
## 433 12.03 16.1
## 434 16.22 14.3
## 435 15.17 11.7
## 436 23.27 13.4
## 437 18.05  9.6
## 438 26.45  8.7
## 439 34.02  8.4
## 440 22.88 12.8
## 441 22.11 10.5
## 442 19.52 17.1
## 443 16.59 18.4
## 444 18.85 15.4
## 445 23.79 10.8
## 446 23.98 11.8
## 447 17.79 14.9
## 448 16.44 12.6
## 449 18.13 14.1
## 450 19.31 13.0
## 451 17.44 13.4
## 452 17.73 15.2
## 453 17.27 16.1
## 454 16.74 17.8
## 455 18.71 14.9
## 456 18.13 14.1
## 457 19.01 12.7
## 458 16.94 13.5
## 459 16.23 14.9
## 460 14.70 20.0
## 461 16.42 16.4
## 462 14.65 17.7
## 463 13.99 19.5
## 464 10.29 20.2
## 465 13.22 21.4
## 466 14.13 19.9
## 467 17.15 19.0
## 468 21.32 19.1
## 469 18.13 19.1
## 470 14.76 20.1
## 471 16.29 19.9
## 472 12.87 19.6
## 473 14.36 23.2
## 474 11.66 29.8
## 475 18.14 13.8
## 476 24.10 13.3
## 477 18.68 16.7
## 478 24.91 12.0
## 479 18.03 14.6
## 480 13.11 21.4
## 481 10.74 23.0
## 482  7.74 23.7
## 483  7.01 25.0
## 484 10.42 21.8
## 485 13.34 20.6
## 486 10.58 21.2
## 487 14.98 19.1
## 488 11.45 20.6
## 489 18.06 15.2
## 490 23.97  7.0
## 491 29.68  8.1
## 492 18.07 13.6
## 493 13.35 20.1
## 494 12.01 21.8
## 495 13.59 24.5
## 496 17.60 23.1
## 497 21.14 19.7
## 498 14.10 18.3
## 499 12.92 21.2
## 500 15.10 17.5
## 501 14.33 16.8
## 502  9.67 22.4
## 503  9.08 20.6
## 504  5.64 23.9
## 505  6.48 22.0
## 506  7.88 11.9

Now the data set is contained in the object Boston. Read about the data set:

?Boston

How many rows are in this data set? How many columns? What do the rows and columns represent?

nrow(Boston) # 506

## [1] 506

length(Boston) # 14 columns

## [1] 14

The rows represent suburbs of Boston, and each column is a different variable.

Make some pairwise scatterplots of the predictors (columns) in this data set. Describe your findings.

par(mfrow = c(2, 2))
plot(Boston$nox, Boston$medv)
plot(Boston$rm, Boston$indus)
plot(Boston$age, Boston$black)
plot(Boston$dis, Boston$crim)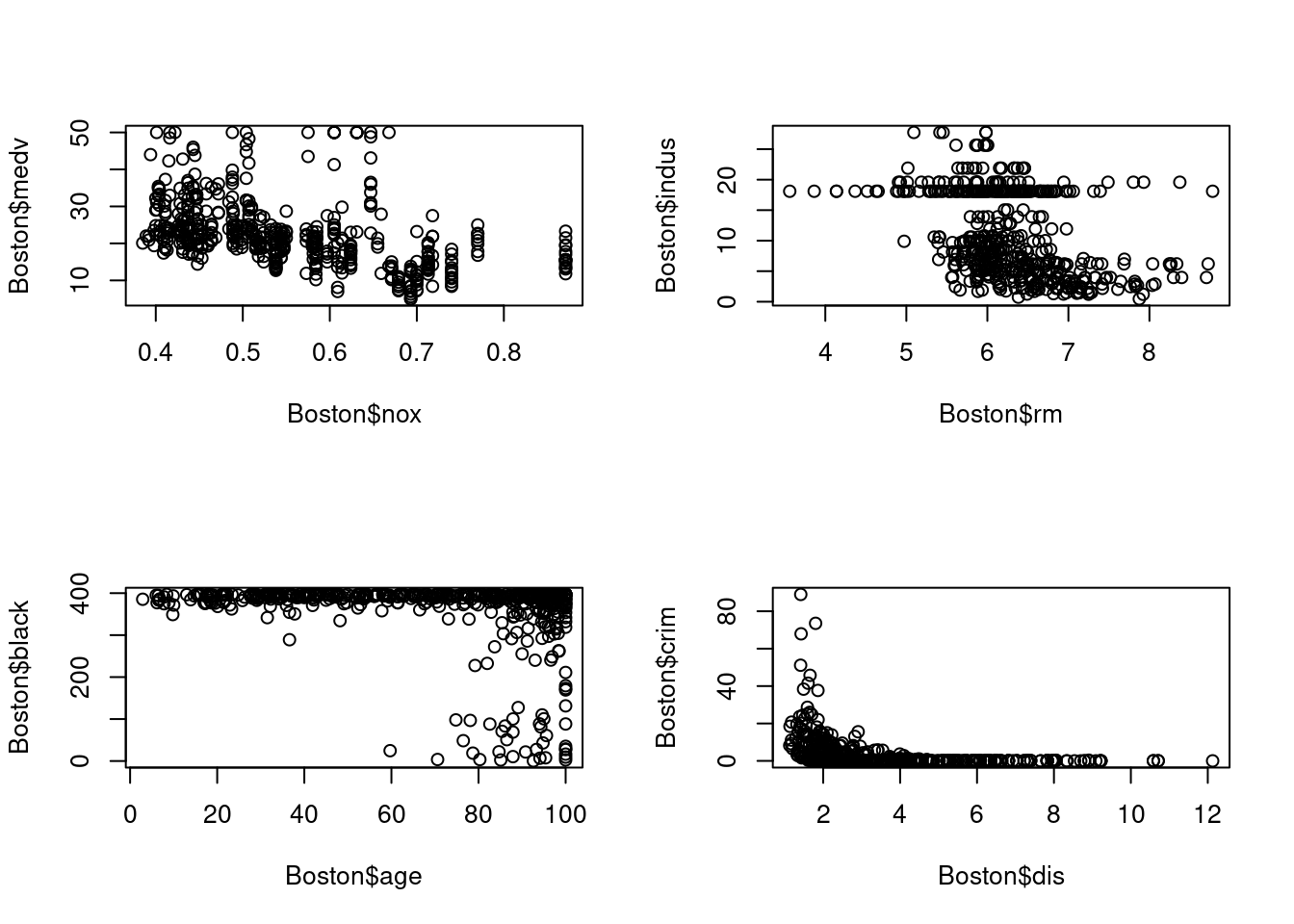

Are any of the predictors associated with per capita crime rate? If so, explain the relationship.
Do any of the suburbs of Boston appear to have particularly high crime rates? Tax rates? Pupil-teacher ratios? Comment on the range of each predictor.

hist(Boston$crim)

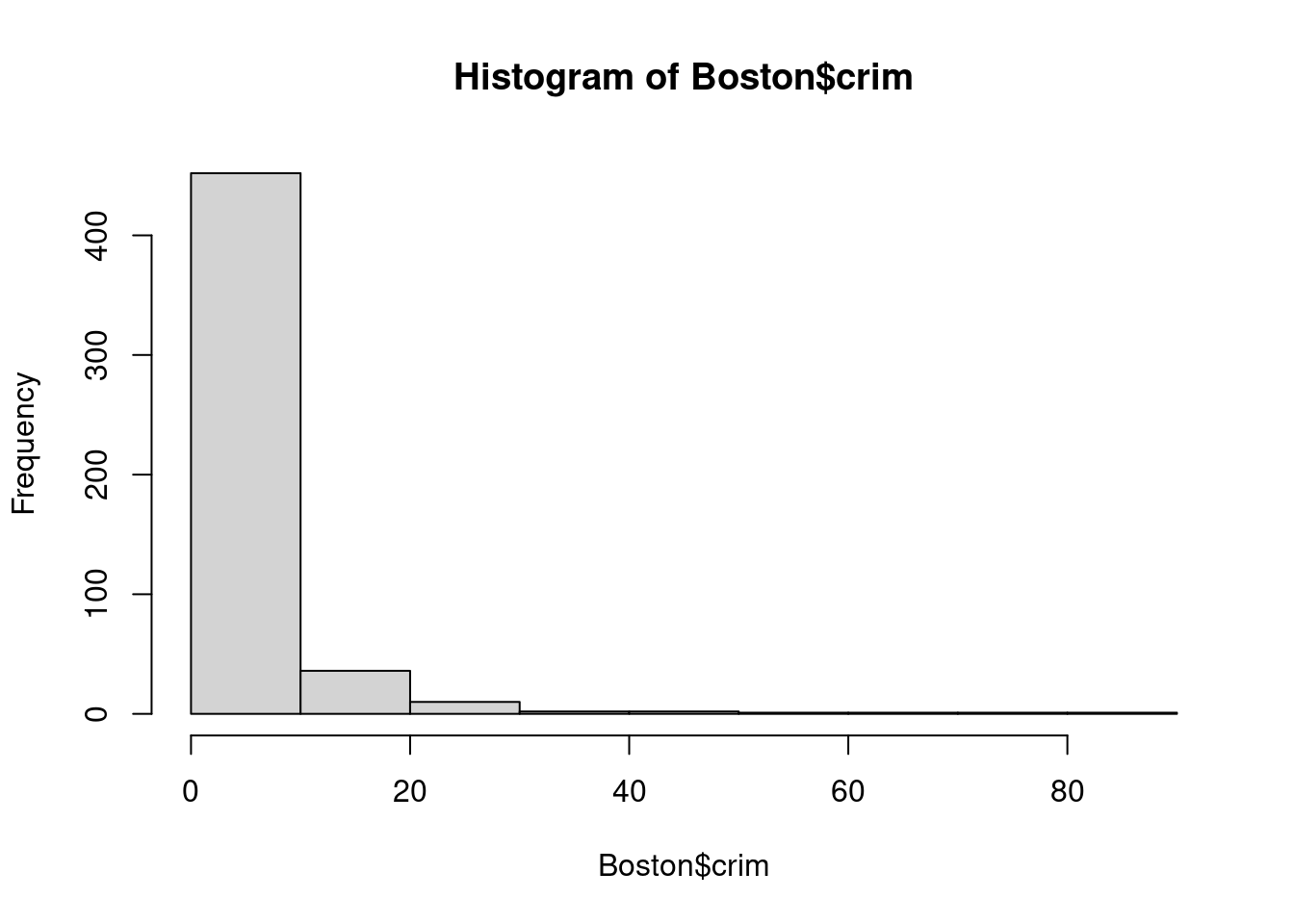
How many of the suburbs in this data set bound the Charles river?

sum(Boston$chas)

## [1] 35